Driehoek, omgeschreven cirkel en oppervlakte

Bewijs: de vermenigvuldiging van de zijden van een driehoek gedeeld door 4x de straal van de omgeschreven cirkel is gelijk aan de oppervlakte

dus abc/4r=opp ABC

a= |BC|, b= |AC|, c=|AB|, r=straal omgeschreven driehoek

Dorien
Leerling bovenbouw havo-vwo - donderdag 28 februari 2002

Antwoord

Eerst maar eens een plaatje:



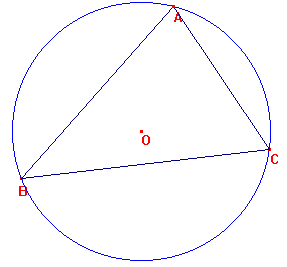
Teken de hoogtelijn AD van ABC. Teken de lijn AK door O, KC en AC.



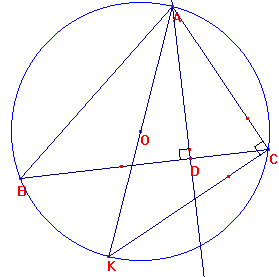
ABD is gelijkvormig met AKC.
Immers, ADB=ACK en ABC=AKC (waarom?)
AB : AK = AD : AC
AD = AB·AC/AK = AB·AC/2r

Opp(ABC)=BC·AD/2
Opp(ABC)=BC·(AB·AC/2r)/2=AB·BC·AC/4r

Zie Formule van Heron | drie andere formules

vrijdag 1 maart 2002

Re: Driehoek, omgeschreven cirkel en oppervlakte

©2001-2024 WisFaq