Een hulpstelling van Saccheri

De som van de hoeken in een driehoek is kleiner dan of gelijk aan 180 graden.

Saccheri had de volgende hulpstelling nodig om he bovenstaande te bewijzen:
D is het midden van BC en E is het unieke punt op het verlengde van AD waarvoor geld dat A, D en E op één lijn liggen en AD=DE.
Dan geldt dat de hoekensom van driehoek AEC gelijk is aan de hoekensom van driehoek ABC en hoek A1 of hoek E is kleiner of gelijk aan 1/2hoek A12.

wat is het bewijs voor deze hulpstelling?

chris
Leerling bovenbouw havo-vwo - maandag 24 november 2003

Antwoord

De stelling
A + B + C = 180°
waarin A, B, C de hoeken zijn van driehoek ABC staat bekend als de Stelling van Saccheri-Legendre.
Het bewijs van deze stelling is nogal gecompliceerd omdat daarbij het zogenoemde Axioma van Archimedes (continuïteitsaxioma) nodig is.
Of Saccheri de genoemde Hulpstelling inderdaad gebruikt heeft weet ik niet, maar, om het bewijs van de naar hem genoemde stelling te leveren, kan de hulpstelling wel dienen.
Die hulpstelling laat zien, dat het mogelijk is een driehoek te construeren die dezelfde hoekensom heeft als driehoek ABC, maar waarin een hoek kleiner of gelijk is aan de helft van hoek A.
Voor het bewijs zie onderstaande tekening.

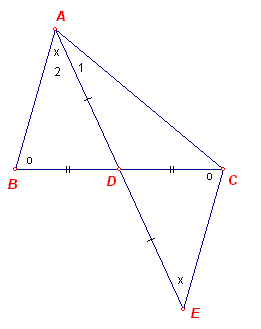
De driehoeken ABD en ECD zijn congruent (ZHZ), immers AD = ED, BD = CD, hoek D = hoek D.
Daaruit volgt direct dat A₂ = AEC = E.
Nu is
A = BAC = A₁ + A₂, zodat
A = A₁ + E
En dan is duidelijk dat
A₁ = ¹/₂A OF E = ¹/₂A

dinsdag 25 november 2003

©2001-2024 WisFaq