Kansverdeling roulette

Hoeveel keer moet er gespeeld worden (gemiddeld) met een waarschijnlijkheid van 95% resp. 97,5% bij roulette om 36 (van de 37) verschillende "getallen" te krijgen. Wat is de formule om dit te berekenen? b.v.na 60X zijn er 31 getallen verschenen, 24 getallen zijn vaker dan 1x geraakt, sommige 3x, 6 getallen zijn nog niet geraakt.

Ton Sm
Iets anders - woensdag 29 oktober 2003

Antwoord

Een van de problemen die je hierbij tegenkomt, is het feit dat die waarschijnlijkheid helemaal niet in de buurt van 95% hoeft te komen.
Ik ben er daarom maar van uit gegaan, dat het gaat om: tenminste 36 vakjes geraakt na n keer spelen. Dan weet je zeker dat deze kans naar 1 gaat naderen als n naar oneindig gaat.
Even een eenvoudiger voorbeeld.
Neem een roulette-spel met maar 5 vakjes.
Je speelt 10 keer.
Hoe groot is de kans dat je 4 van de 5 vakjes geraakt hebt (en 1 vakje dus niet).
Je telt het aantal(#) 'goede' rijtjes, en deelt door het totaal aantal rijtjes.
#goed = 5 maal
#(zonder 1)
- #(zonder 1 en 2) - #(zonder 1 en 3) - #(zonder 1 en 4) - #(zonder 1 en 5)
+ #(zonder 1 en 2 en 3) + ...
- #(zonder 1 en 2 en 3 en 4) - ...

Uitwerking van al deze berekeningen levert de formule:
#goed = 5·4¹⁰ - 5·(4 boven 3)·3¹⁰ + 5·(4 boven 2)·2¹⁰ - 5·(4 boven 1)·1¹⁰

Dan de kans dat je alle vakjes geraakt hebt na 10 keer spelen.
#goed = 5¹⁰ - (5 boven 4)·4¹⁰ + (5 boven 3)·3¹⁰ - (5 boven 2)·2¹⁰ + (5 boven 1)·1¹⁰

Het totaal aantal rijtjes is gelijk aan 5¹⁰.
Hiermee is dus de kans bekend.

Dit kun je generaliseren naar de situatie van n keer spelen.
Stel het gaat om een roulette met a+1 mogelijke uitkomsten.
Noem f(n) de kans dat na n keer spelen precies a vakjes getroffen zijn.
Noem g(n) de kans dat na n keer spelen precies alle a+1 vakjes getroffen zijn.
Dan geldt:

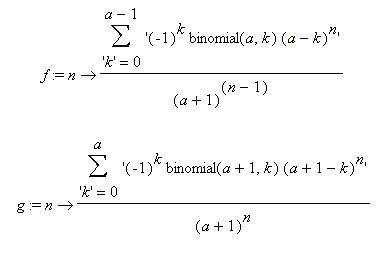
Neem nu a=36.
Bekijk de grafiek van f(n) en die van f(n)+g(n)

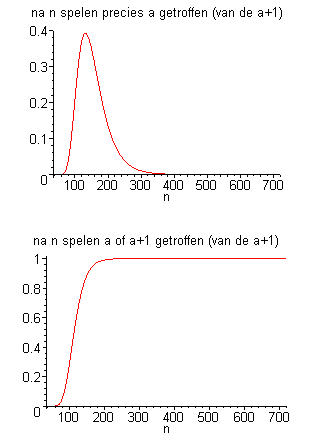
Je ziet dat f(n) niet boven 0.4 komt.

f(n)+g(n) gelijkstellen aan 0.95 levert dan een vergelijking waaruit n numeriek te benaderen is.
Voor de situatie van a=36, dus 37 rouletteuitkomsten, waarvan er tenminste 36 geraakt moeten zijn (met een kans van 95%) kom ik (met behulp van Maple) uit op 168 keer spelen.
groet,

zaterdag 1 november 2003

©2001-2024 WisFaq