
Standaarddeviatie
De ABN/AMRO bank verstrekte gegevens van een steekproef van de gemiddelde bedragen die 10 studenten uitgaven in de zomervakantie van 2003:
Cumulatief % Aantal studenten (absoluut) Gem.aantal €
20% 2 €1.200,--
60% 4 €1.500,--
80% 2 €1.800,--
100% 2 €2.000,--
Wat is nu de standaarddeviatie van het gemiddeld bestede bedrag aan euro's?
Het antwoord moet 290,59 zijn, en ik kom maar niet op dat bedrag, kunt u me aub helpen?
Tamara
Student hbo - donderdag 23 oktober 2003
Antwoord
Bepaal eerst het gemiddelde bedrag, dat is (2·1200 + 4·1500 + 2·1800 + 2·2000)/10 = 1600.
De formule van de standaarddeviatie bij een steekproef luidt
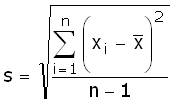
Eerst gaan we de som bepalen, dat is 2·(1200-1600)2+4·(1500-1600)2+2·(1800-1600)2+2·(2000-1600)2 = 760 000.
Dit moeten we delen door het aantal waarnemingen - 1, in ons geval dus 9, dan kom je op 84 444,44... en hiervan moeten we de wortel nemen, en dan kom je inderdaad afgerond op 290,59 uit.

donderdag 23 oktober 2003
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|