Oppervlakte van een driehoek met integralen

Bereken m.b.h.van integralen de oppervlakte van de driehoek abc met als zijden
A- y= 5x+10
B- y= -3x+6
C- y=x-10

Ine Va
3de graad ASO - vrijdag 17 oktober 2003

Antwoord

Beste Ine,

Eerst maar een tekening.

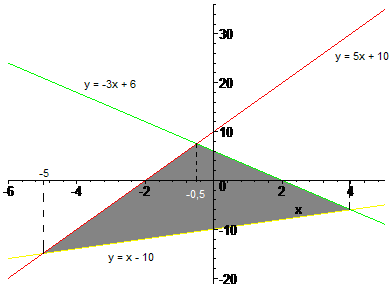
De snijpunten van de functies moet je zelf kunnen vinden (het zijn allemaal eerstegraadsfuncties dus dat zou geen probleem mogen zijn).
We gaan eerst de oppervlakte onder de x-as van -5 tot 4 van de gele grafiek (y=x-10) bepalen.
_-5ò⁴(x-10)dx = _-5ò⁴x dx - 10_-5ò⁴dx
=
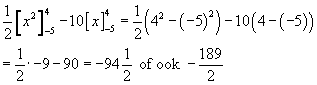
Maar een oppervlakte kan nooit negatief zijn, dus |-94,5| = 94,5. Maar dan hebben we teveel geïntegreerd, want nu zitten de groene driehoekjes bij de oppervlakte, dus die moeten er nog van afgetrokken worden.

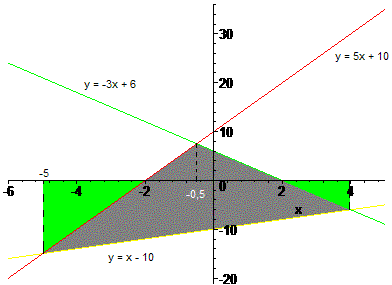
De groene driehoek links heeft als stippellijn (basis) de lengte 15 (vul maar -5 in de gele functie in), en als hoogte 3, dus oppervlakte ¹/₂·15·3 = 22¹/₂. De groene driehoek rechts heeft als stippellijn 6 (basis) en als hoogte 2, dus oppervlakte is ¹/₂·6·2 = 6. Dus in totaal moet er 22¹/₂ + 6 = 28¹/₂ van de oorspronkelijke oppervlakte afgetrokken worden, dus 94¹/₂ - 28¹/₂ = 66. Je zou ook in plaats van de oppervlakteformule van een driehoek, van -5 tot en met -2 van de rode grafiek kunnen integreren (aangezien oppervlakte absolute waarde nemen), en van 2 tot en met 4 van de groene grafiek integreren, en wederom absolute waarde nemen. En het totaal aftrekken van de reeds gevonden oppervlakte van de gele grafiek van -5 tot en met 4.

Maar dat is alleen de oppervlakte onder de x-as. Er is ook nog een stuk boven de x-as. Namelijk een driehoekje van -2 tot en met -0,5 van de rode grafiek (y=5x+10), en nog een driehoekje van -0,5 tot en met 2 van de groene grafiek (y=-3x+6). Bereken nu zelf de oppervlaktes van de driehoekjes (hetzij via integreren, hetzij via oppervlakteformule driehoek) boven de x-as en tel de oppervlaktes op bij de 66.

Lukt het zo?

Groetjes,

Davy.

vrijdag 17 oktober 2003

©2001-2024 WisFaq