Bewijs dat de som van de hoeken van een driehoek 180º is

Ik zit in de tweede klas VWO. Bij wiskunde worden de dingen niet echt bewezen. Ik heb geprobeert om een bewijs te maken. Kunnen jullie kijken of dit een goed bewijs is en of het ook gemakkelijker kan? Ik ben er een hele ijd mee bezig geweest. De plaatjes zijn helaas weggevallen, maar die kan ik wel mailen als julie dit willen...
Groeten, Jan.

Deel 1

Twee snijdende lijnen, met de hoeken a,b c en d

$\angle$ a + $\angle$ b = 180º (hoek a + hoek b)
$\angle$ b + $\angle$ c = 180º
Dus $\angle$ a = $\angle$ c

1a: De som van de hoeken van twee lijnen die bij het snijpunt naast elkaar liggen is 180º.

1b: De tegenoverliggende hoeken bij het snijpunt van twee lijnen zijn gelijk.

Deel 2.
Vierhoek ABCD is een rechthoek. De hoeken van een rechthoek zij 90º. De tegenoverliggende zijden van een rechthoek lopen parallel (een rechthoek is een speciaal parallellogram).

Maak op zijde AB punt E met afstand AE = BE (E ligt in het midden)
Trek door E een lijn die niet evenwijdig loopt aan AB en ook niet aan AC.
Je krijgt D(riehoek)AEF en D BEG.
$\angle$AEF = $\angle$BEG (= a) (volgt uit bewijs 1a)
AE = EB (E ligt in het midden van AB)
$\angle$FAE = 90º = $\angle$BGE
dus: DAEF = D BEG.
Dus $\angle$AEF = $\angle$BEG (= b)

2. Lijn AF loopt evenwijdig aan lijn BG. Deze twee evenwijdige lijnen worden gesneden door lijn GF. De hoeken rond beide snijpunten zijn gelijk. Uit 1b volgt dat de som van de hoeken die bij de snijpunten naast elkaar liggen = 180º

Deel 3:
Een parallellogram bestaat uit twee paar evenwijdige lijnen. Uit 2 volgt dat de som van de hoeken die naast elkaar liggen = 180º , dat de hoeken die tegenover elkaar liggen gelijk zijn en dat de som van de hoeken van een parallellogram 360º is.

Deel 4.
Teken een driehoek ABC.

Spiegel de driehoek vond punt A zodat je driehoek A’B’C’ krijgt.

Schuif de driehoeken aan elkaar vast zodat AB en B’A’ samenvallen.

Vierhoek ACBC’ is een parallellogram omdat:
- de tegenoverliggende hoeken gelijk zijn
- de hoek van AC’ met AB (= b) gelijk is aan de hoek van CB met AB. Dus AC’ loopt evenwijdig aan CB
- de hoek van BC’ met AB (= a) gelijk is aan de hoek van CA met AB. Dus BC’ loopt evenwijdig aan CA.

Dit kan je met elke driehoek doen.

Bewijs:
Van elke driehoek kan je een parallellogram maken door een gespiegelde driehoek eraan vast te maken.
De som van de hoeken van dat parallellogram is gelijk aan de som van de hoeken van die twee driehoeken.
De som van de hoeken van een driehoek en de som van de hoeken van de gespiegelde driehoek is gelijk.
De som van de hoeken van een parallellogram is 360º.

Dus: de som van de hoeken van een driehoek is dus de helft van de som van de hoeken van een parallellogram = 180º.

Jan Ha
Leerling onderbouw vmbo-havo-vwo - dinsdag 16 september 2003

Antwoord

Is het goed en kan het simpeler??

In jouw bewijs ga je uit van het feit dat de som van de hoeken van een parallellogram 360° is.
Probleem is dat we moeten afspreken wat we aannemen en wat we vervolgens kunnen bewijzen.
Meestal gaan we uit van de afspraak:
een gestrekte hoek is 180°.
Om nu te bewijzen dat de hoeken van een vierhoek samen 360° zijn, zouden we eigenlijk eerst moeten bewijzen dat de hoeken van een driehoek samen 180° zijn!

Dat bewijs kan op de volgende manier:
Ken je de begrippen F- en Z-hoeken?
Dat is ook zo'n basisafspraak:
Het gaat in beide gevallen om twee evenwijdige lijnen gesneden door een derde lijn.

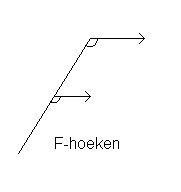
In de figuren staat aangegeven welke hoeken dan gelijk zijn.
Nu het bewijs dat de hoeken van een driehoek samen 180° zijn.

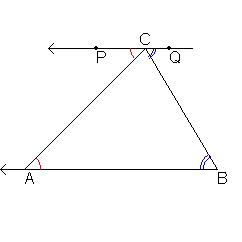
Trek door C een lijn evenwijdig met AB.
Volgens Z-hoeken geldt dan
$\angle$BAC=$\angle$ACP
$\angle$ABC=$\angle$BCQ

Nu geldt:
$\angle$ACP+$\angle$ACB+$\angle$BCQ=180°
(immers P,C en Q liggen op één lijn: $\angle$PCQ is een gestrekte hoek)
dus......volgens mij kun je het nu wel afmaken.

dinsdag 16 september 2003

Re: Bewijs dat de som van de hoeken van een driehoek 180º is

©2001-2024 WisFaq