Partiële integratie

Kan u mij een korte duidelijke theoretische uitleg geven over partiële integratie, want in mijn cursussen vindt ik geen duidelijke uitleg? Dank bij voorbaat

Tom De
Student universiteit - dinsdag 2 september 2003

Antwoord

Het begint met een goed begrip van differentiëren, en dan in dit geval vooral de productregel.

(f·g)' = f'·g + f·g'

Beide kanten integreren levert:

[f·g] = ò(f'·g)dx + ò(f·g')dx

Die rechte haken om f·g betekent dat er nog rekening gehouden moet worden met een eventuele constante.
Deze formule kun je ook zo schrijven:

ò(f'·g)dx = [f·g] - ò(f·g')dx

Wat heb je hier nu aan?
De winst zit hem in het feit dat je van een integraal met een functie g erin, een nieuwe integraal maakt met daarin de functie g', die meestal eenvoudiger is. De prijs die je betaalt zit hem in de functie die in het begin f' genoemd wordt, en die uiteindelijk terecht komt in de integraal als functie f.

Een voorbeeld: de functie x·cos(x) moet geintegreerd worden.
Kies in dit geval: g(x) = x en f'(x) = cos(x).
Dan is f(x) = sin(x)
Dan krijg je dus:



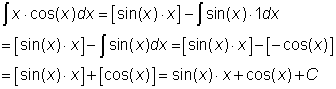
In de praktijk zit de moeilijkheid meestal in de keuze van g en f'. Door oefening en ervaring krijg je hier handigheid in.
succes,

dinsdag 2 september 2003

©2001-2024 WisFaq