Cirkel en rechte

y=x+a snijdt cirkel volgens een koorde met lengte Ö2
Vgl. cirkel; x²+y²=25
Mijn vraag is, kan je hieruit de vgl. van de snijdende rechte vinden, de snijpunten met de cirkel en de raaklijn aan de cirkel die evenwijdig is aan de gegeven rechte?
Volgens mij is de vgl. van de snijdende rechte y=x+7.
Maar dit ben ik op een niet katholieke manier bekomen.
Uit de richtingscoëfficiënt van de rechte(1=45°) en wetende datÖ2 de schuine zijde is van een driehoek met twee zijdes gelijk aan 1 en een tekeningetje heb ik y=x+7 gevonden. Is dat juist en hoe kom je daar normaal aan? En hoe kom je dan aan de snijpunten en de raaklijn?
Alvast dank!
Bea

Bea Ve
Student Hoger Onderwijs België - maandag 18 augustus 2003

Antwoord

Je hebt het goed. Al zijn er twee mogelijkheden. (+ en - 7)

Snijd eerst de rechte en cirkel:
y=x+a
x²+y²=25

=
x²+(x+a)²=25

Deze vergelijking geeft alle x-waarden voor snijpunten van rechten van de vorm y=x+a met de cirkel x²+y²=25

Een bijkomde voorwaarde is dat de afstand tussen de punten Ö2 moet zijn. Aangezien de rechte als richting 1 heeft is dus de afstand tussen de x coordinaten (en ook tussen de y-coordinaten) gelijk aan 1. Want Ö(1²+1²) = Ö2

Los de bovenstaande vierkantsvergelijking op en stel de eis dat de beide antwoorden 1 moetn verschillen.

Concreet:
x_1 := - 1/2 a + 1/2 Ö(-a² + 50)
x_2 := - 1/2 a - 1/2 Ö(-a² + 50)


en x_1-1=x_2

of

-1/2 a+1/2 Ö(-a²+50)-1 = -1/2 a-1/2 Ö(-a²+50)

En dus a=7 of a=-7

Dus de rechten:

y=x+7 en y=x-7

De exacte snijpunten met de cirkel zijn nu niet meer moeilijk hé.


De raaklijn evenwijdig aan die rechte is al helemaal niet moeilijk. Een raaklijn staat loodrecht op de middelijn door het raakpunt. De raaklijn moet richting 1 hebben.
De loodrechte richting (van de middellijn dus) is dan -1 (want m1*m2=-1) en de middellijn moet door het centrum (0,0)

Dus de bijhorende middellijn is y=-x

Deze snij je met de cirkel om het raakpunt te bepalen. Een je het raakpunt hebt is het niet moeilijk meer.

Enkele figuren:
De cirkel en de rechte y=x+7


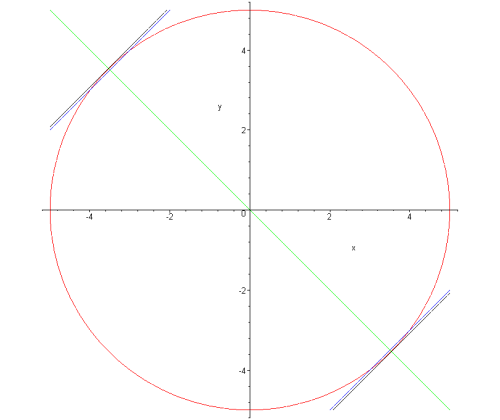
Rood: Cirkel
Groen: Middellijn loodrecht op rechten y=x+/-7
Blauw: De rechten y=x+/-7
Zwart: De raaklijnen.






Koen Mahieu

maandag 18 augustus 2003

©2001-2024 WisFaq