Terrasbezoek: hoe waarschijnlijk dat je op alle stoelen zat na zoveel bezoeken?

"Er zijn 100 stoelen op een terras. Het terras bezoek je 143 keer. Bij elk bezoek kies je willekeurig een stoel uit. Wat is de kans dat je op elke stoel minstens een keer hebt gezeten?"

Ik kwam met het volgende antwoord maar ik vraag me af of het goed is:

-------------------

Aantal bezoeken = 143
Aantal stoelen = 100

Kans dat je stoel 1 kiest tijdens een bezoek: P(stoel 1) = 1/100
Kans dat je stoel 2 kiest: P(stoel 2) = 1/100
...
Kans dat je stoel 100 kiest: P(stoel 100) = 1/100

Ok, als we nu bij bezoek 1 stoel 1 kiezen, en bij bezoek 2 stoel 2, etc, dan maakt naar 100 bezoeken het niet meer uit welke stoel we dan kiezen, want we hebben alle stoelen al een keer uitgekozen. De kans dat we dit zo kiezen is:

P = (1/100)^100 * 1^43 = 1,e-200

Om de kans te berekenen dat je alle stoelen een keer hebt uitgekozen, ongeacht de volgorde, moeten we eerst het aantal mogelijkheden berekenen dat je deze stoelen kan kiezen...

100 verschillende keuzes. 43 maakt-niet-uit keuzes.

Aantal mogelijkheden:

143! / 43! = 6,3797962993837354473687420471909e+194

Dus we hebben de kans op 1 mogelijkheid en we hebben het aantal mogelijkheden... Deze twee getallen vermenigvuldigen:

P(Alle stoelen een keer uitgekozen) = 6,3797962993837354473687420471909e+194 * 1,e-200 = 6,3797962993837354473687420471909e-6

-------------------

Raynor
Student universiteit - donderdag 7 augustus 2003

Antwoord

Eerst even zien of je redenering kan kloppen...

Stel je voor dat je 143 ticketjes hebt, genummerd: 1, 2, … tot 143. Bij elk bezoek leg je een ticketje op een stoel. Omdat je bij elk van de 143 bezoeken kan kiezen uit 100 verschillende stoelen, zijn er zo 100¹⁴³ verdelingen mogelijk.

We bekijken nu hoeveel ‘gunstige’ gevallen er zijn, waar er dus op elk van de 100 stoelen minstens 1 ticketje ligt na 143 bezoekjes.
Uit de 143 verschillende tickets moeten we er 100 vastzetten. 143 manieren voor de eerste stoel, 142 voor de tweede stoel, … 44 manieren voor de 100-ste stoel. We kunnen er dus 100 vastzetten op 143!/43! manieren. De resterende 43 kunnen we op 100⁴³ manieren verdelen over de 100 stoelen. Er zijn dus 143!/43 !.. 100⁴³ gunstige gevallen.

De kans dat je na 143 alle stoeltjes bezet hebt is dus: 143!/43 !. 100⁴³/ 100¹⁴³ = 143!/[43 ! .100¹⁰⁰] = 143/100.142/100. … . 44/100 = 6.380E-06. Dit is precies het resultaat dat jij ook vond.

Dit laatste product kan je uitrekenen in Excel. Je kan dan ook simuleren dat je na 155 bezoekjes een kans van 3.772 zou hebben... Dit is uiteraard nonsense omdat een kans nooit 1 kan worden ! Met andere woorden : de redenering is fout… De onderliggende reden is dat we onze ‘gunstige’ gevallen meervoudig geteld hebben als samenstellingen van 100 ‘vaste’ en 43 ‘vrije’ keuzes. Via een andere redenering kom jij ook op eenzelfde formule uit die voor grotere aantallen bezoeken ook door het dak gaat…

Daarom een tweede poging. We beginnen met een voorbeeldje: 2 stoelen, 3 bezoekjes, mogelijkheden: {1,2,3}{}, {1,2}{3}, {1,3}{2}, {1}{2,3}, {2,3}{1}, {2}{1,3}, {3}{1,2} en {}{1,2,3}. De haakjes stellen stoelen voor, elk getal tussen haakjes het zoveelste bezoek. Bemerk dat we een onderscheid maken tussen bijvoorbeeld sequenties {1,2}{3} en {1,3}{2} enerzijds en {1,2}{3} en {3}{1,2} anderzijds. In 6 van de 8 gevallen is er dus minstens één stoel bezet. Intuïtief komt dit volgens mij het best overeen met de realiteit van terrasbezoek.

Iets formeler nu. Op het terras staan er m stoeltjes en we bezoeken het terras n keer. Bij elk van de n bezoeken kunnen we uit m stoelen kiezen. Er zijn dus mⁿ mogelijke sequenties van onze bezoeken. Dit klopt inderdaad voor ons voorbeeldje: 2³=8 en we vonden 8 mogelijke sequenties.

We definiëren T(n,m) als het aantal manieren om met n bezoekjes precies m stoelen te bezetten. Hierbij moeten we heel nauwkeurig vastleggen wat we bedoelen met ‘verschillende’ manieren om dat te doen. Op basis van ons voorbeeld gebruiken we de definitie waarbij we onze bezoeken en stoelen onderscheiden.

We zien:
Als nm, dan moet T(n,m)=0 want we kunnen met minder dan m bezoekjes onmogelijk alle m de stoelen bezetten.

Als m=1, dan is T(n,m)=1 want de enige mogelijke sequentie is [1,2, .., n]

Als n=m, dan is T(n,m)=n!=m!. Bijvoordeeld: T(3,3)=6 want alle mogelijke sequenties zijn: {1}{2}{3}, {1}{3}{2}, {2}{1}{3}, {3}{1}{2}, {2}{3}{1} en {3}{2}{1}.

Als n m dan bekijken we de sequenties van n-1 bezoekjes en proberen die uit te breiden met het n-de bezoek. We kunnen de sequenties van n-1 bezoeken splitsen in 2 groepen: die waarbij we met de eerste n-1 bezoekjes alle m stoelen al bezet hadden en die waarbij we met n-1 bezoekjes niet alle m stoelen bezet hadden.

In ons voorbeeld zijn dit de goede sequenties met n=3:
{1,2}{3}, {1,3}{2}, {1}{2,3}, {2,3}{1}, {2}{1,3}, {3}{1,2}.
Gesplitst in 2 groepen:
{1,3}{2}, {1}{2,3}, {2,3}{1}, {2}{1,3} : afgeleid uit sequenties {1}{2} en {2}{1}
{1,2}{3}, {3}{1,2} : afgeleid uit sequentie {1,2}
Zodat : T(3,2)=2.T(2,2)+2.T(2,1)=2.2+2.1=6.

Van het eerste geval zijn er T(n-1,m) gevallen. Bij het n-de bezoek kunnen we een willekeurige stoel kiezen. Er zijn dus telkens m mogelijke manieren om aan te vullen tot een gunstige bezetting in n bezoeken.
In het tweede geval zijn we enkel geïnteresseerd in die situaties waarbij we met het n-de bezoek alle m stoelen genomen hebben. Tijdens het n-1 de bezoek moeten we dus precies m-1 stoelen al gebruikt hebben en dit kan op m.T(n-1,m-1) manieren. Er is maar 1 manier om daarna in n bezoeken alle stoelen te bezetten, namelijk door tijdens het n-de bezoek op de onbezette stoel te gaan zitten.
Zodat in het algemeen: T(n,m)=m.T(n-1,m) + m.T(n-1,m-1)=m.( T(n-1,m)+T(n-1,m-1))

(bemerk dat je hieruit onmiddellijk afleidt dat T(n,n)=n!)

De kans dat we met n bezoekjes alle m stoelen bezetten is dus
t(n,m) = T(n,m)/mⁿ =
T(n-1,m)/m^n-1 + T(n-1,m-1)/m^n-1 =
t(n-1,m) + (m-1)^n-1/m^n-1.T(n-1,m-1)/(m-1)^n-1 =
t(n-1,m) + (1-1/m)^n-1.t(n-1,m-1)

Met als randcondities : t(n,m)=0 als nm en t(n,1)=1.

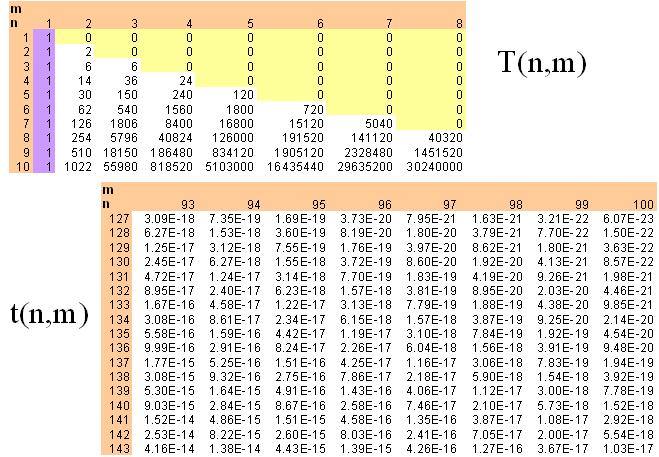
In Excel kan je dit tamelijk makkelijk uitrekenen. In de figuur vind je een paar extracten voor T(n,m) en t(n,m). De gevraagde kans is dus ongeveer 1.03E-17.



Interessante aanvullende vragen :
- wat is het verwacht aantal verschillende stoelen waarop je zat na n bezoekjes?
- wat is het meest waarschijnlijk aantal bezoekjes dat je moet plegen opdat je alle stoeltjes minstens één keer zou gehad hebben?
- hoeveel bezoekjes zijn er nodig om met een waarschijnlijkheid van 50% te kunnen zeggen dat je op alle stoeltjes zat?
- wat met alternatieve interpretaties van identieke bezoek-sequenties? Link naar StirlingNumber of the Second Kind
- simulatie om model voor terrasbezoek te bevestigen?

Groetjes,
Johan

andros
maandag 1 september 2003

©2001-2024 WisFaq