Perspectiefberekening

Hallo,

Ik kwam een vraag tegen en ik kon het niet zelf oplossen, dus ik hoop dat het wel oplosbaar is.
De vraag is: persoon A is drie meter verder van persoon B.
Persoon A heeft een lengte van twee meter. Als persoon A naar persoon B kijkt, dan het lijkt voor persoon A alsof persoon B een lengte heeft van een meter. Hoe lang is persoon B in werkelijkheid?

Met vriendlijke groeten

Masih
Leerling bovenbouw havo-vwo - zondag 3 augustus 2003

Antwoord

Je opgave is onduidelijk. Probeer zelf eens een betekenis te geven aan de zin 'Het lijkt voor persoon A alsof persoon B een lengte heeft van een meter'.

Je zou je kunnen inbeelden dat persoon A een liniaal voor zich uit en 'naast' persoon B houdt en zo een of andere schijnbare lengte afleest. Die lengte is dan wel afhankelijk van de afstand waarop het liniaal wordt vastgehouden! (Extreme voorbeelden: hou het liniaal tegen je oog, en de persoon lijkt 3cm te zijn, hou het liniaal tegen persoon B en de persoon lijkt zijn ware lengte)

Jouw uitspraak heeft dus geen betekenis als de lengte waarop het (ingebeelde) liniaal niet wordt opgegeven. Waar je wel genoeg aan hebt, is de hoek waaronder persoon B door persoon A wordt gezien. Die hoek is de vertaling van de evenredigheid tussen 'afstand persoon A - liniaal' en 'schijnbare lengte persoon B'.

Het probleem wordt dus het volgende:



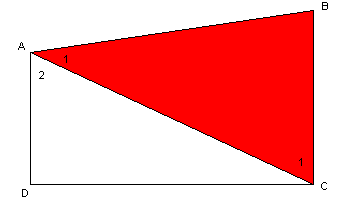
A1 en A2 zijn gekende hoeken. A1 is opgegeven en A2 is bgtg(3/2).

|AD|=2
|DC|=3
|AC|=√13 (Pythagoras)

AC snijdt de evenwijdigen AD en BC. Daarom is C1=A2. De hoek B kan nu ook gevonden worden als 180-A1-C1. We kunnen nu in de driehoek ABC de sinusregel toepassen.

sin(A1)/|BC| = sin(B)/|AC|

zodat

|BC|=|AC|.sin(A1)/sin(B)=|AC|.sin(A1)/sin(A1+A2)

maandag 4 augustus 2003

©2001-2024 WisFaq