Re: Limieten berekenen

Dit is een reactie op vraag 13101

Hallo wisfaq,

Bedankt voor uw reactie, ik zit in 5 vwo en ken de regel van l'hopital nog niet, dit zijn de standaardlimieten die ze in mijn boek drukken.



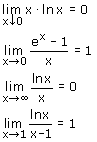
Gek genoeg kan ik deze standaardlimieten nergens vinden op mijn formulekaart havo/vwo, de standaardlimieten zullen wel kloppen,maar volgens zijn die standaardlimieten niet zo bekend of gebruikt men iets anders zoals u zei de regel van l'hopital om dit soort limieten te berekenen, kunt u me dat leren door gebruik te maken van mijn limieten die ik eerder had verzonden ?

Zafarp
Leerling bovenbouw havo-vwo - maandag 14 juli 2003

Antwoord

ja , ze gebruiken daar de regel van l'hopital voor

neem nu die derde limiet , leidt eens de noemer en de teller af !

(afzonderlijk )

dan krijg je : (1/x)/1

ik heb de teller en noemer afzonderlijk afgeleid en dan krijg ik dit , en vul nu eens x$\to$1 in , dan krijg je , als uitkomst 1 !

dit is de regel van l'hopital in het kort !


hoe werkt dat nu , wel als je limieten moet berekenen en je limiet is 0/0 of 0.$\infty$ of iets dergelijks , dan kun je de regel van l'hopital toepassen en wat zegt die regel nu net : leidt teller en noemer apart af en voila , je hebt een nieuwe limiet en dan zul je wel een uitkosmt vinden , of anders moet je het nog eens afleiden tot je een uitkomst hebt!



dus afleiden als 2 getallen hé!! , dus teller en noemer NIET als 1 breuk afleiden zoals je bij normale afgeleide zou doen!


een ander voorbeeld : (x-1)/(2x-2), berekenen hiervan de limiet met x gaat naar 1 , wel natuurlijk , dit is een banaal voorbeeld , en je kunt die 2 in de noemer uit de haakjes zetten , en dan vereenvoudigen , dan krijg je ¹/₂ MAAR om het u nu aan te tonen gebruik ik de regel van l'hopital , wat doe ik : ik leid de teller af en dat is : x , dan leid ik de noemer af en dat is 2

dan heb ik x/2 met x gaat naar 1 $\Rightarrow$ vul x in en wat krijg je ?

inderdaad ¹/₂ zoals we ook kregen indien ik vereenvoudigd had !


voila , snap je de regel van l'hopital nu min of meer?

Lucilius
maandag 14 juli 2003

©2001-2024 WisFaq