Integreren en primitieven vinden

Hallo wisfaq,

Ik doe zelfstudie en kan niet meer verder omdat ik een aantal opgaven niet helemaal begrijp, ze geven namelijk alleen een aantal standaard primitieven maar geen echte voorbeelden hoe men dat toepast, het gaat om de volgende opgaven.

1) geg: f(x)= 2e^(1/2x) en g(x)= 1/(x+4)

gevr:a) Teken de figuren(dat is geen probleem)
b)De grafieken van f en g, de lijn x=2 sluiten een vlakdeel in.Bereken de oppervlakte van dit vlakdeel.

2)bepaal de primitieven :

g(x)= 2/(x-7) en i(x)=-3/(ln10.x)

Wilt aub niet de theorie uit 6VWO gebruiken zoals de substitutiemethode e.d. ik ben nameijk bezig met 5 VWO en als het kan wilt u dan korte stapjes gebruiken zodat ik u kan volgen vooral bij het primitieven vinden.

Alvast hartelijk bedankt.

Tim
Leerling bovenbouw havo-vwo - maandag 7 juli 2003

Antwoord

Hoi,

1)

b) Zie onderstaande tekening voor de situatieschets

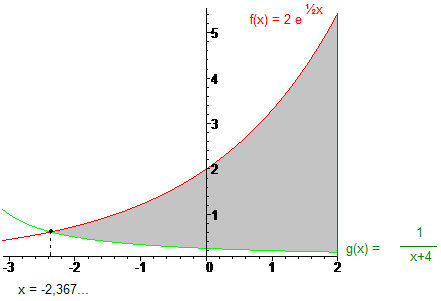
Je ziet dat ik eerst het snijpunt van de twee functies heb bepaald omdat het vlakdeel ingesloten wordt door de functies van f(x) en g(x). Dat snijpunt x -2,367... heb ik gevonden door het snijpunt m.b.v. computerprogramma, maar je kunt het zelf vinden via grafisch rekenmachine ('intersect'-optie). Een exacte algebraïsche oplossing is trouwens onmogelijk.
De oppervlakte die je moet bepalen is het donkergrijze gedeelte, dat wordt ingesloten door f(x), g(x) en x = 2 (groene verticale lijn). De oppervlakte is te berekenen door de rode grafiek te integreren binnen de ondergrens x = -2,367059327 en de bovengrens x = 2, maar dan hebben we een stukje teveel geïntegreerd, namelijk de oppervlakte van de groene grafiek, gaande van x = -2,367059327 tot en met x = 2, dus die oppervlakte moet ervan afgetrokken worden.



2)

Dat mag nu geen probleem meer zijn, je gokt een primitieve differentieert deze en past zo nodig de primitieve aan.

De antwoorden zijn G(x) = 2·ln|x - 7| + c en I(x) = -3·^(ln|x|)/_(ln(10)) + c indien i(x) = ^-3/_(ln(10)·x)

Indien er onduidelijkheden zijn, reageer dan op dit antwoord.

Groetjes,

Davy.

maandag 7 juli 2003

Re: Integreren en primitieven vinden

©2001-2024 WisFaq