Niet homogene lineaire systemen

Met behulp van de algemene homogene oplossing heb ik gevonden:
u1’(t) = [ ¹/₂ sin(bt) + ¹/₂ cos(bt)] * e^(i b t)
u2’(t) = [ ¹/₂ sin(bt) - ¹/₂ cos(bt)] * e^(- i b t)

Ik ben nu op zoek naar u1(t) en u2(t).
Deze twee vergelijkingen komen tot stand vanuit het volgende stelsel:

x’ = | a b | x + | sin(bt) e^(a t) |
| -b a | | cos(bt) e^(a t) |

Hoe kan ik bovenstaande vergelijkingen met zo min mogelijk werk integreren?
Of wordt het echt ingewikkeld?
Had ik de algemene homogene oplossing anders moeten opschrijven dan als volgt:

x(t) = c1 | 1 | e^((a - ib)t) + c2 | 1 | e^((a + ib)t)
| -i | | i |

Met vriendelijke groet,
Bram

Bram
Student universiteit - donderdag 19 juni 2003

Antwoord

Misschien dat de onderstaande hint je verder kan helpen met integreren. Je kunt e.e.a. uitschrijven in redelijk rechttoe-rechtaan naar t-integreerbare brokken:



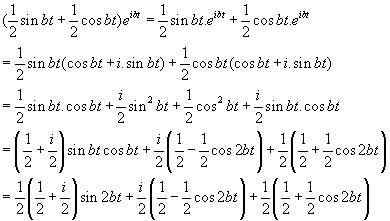
Een dergelijke om-schrijving kun je zelf ook voor u2'(t) maken.

groeten,
martijn

mg
donderdag 19 juni 2003

©2001-2024 WisFaq