Toepassen van de integraal

beste mensen ik heb hier een oud examen sommetje.
ik kom er echt nite uit dan dit, kunnen jullie me even helpen met deze sommetje

op een zekere winterdag (van 0 tot 24 uur) varieert de temperatuur Volgens:
T(t) = 4 sin(p(1-9)/12)+2

Ik moet eerst een grafiek van de temperatuur op deze dag maken???Hoe
ik moet met behulp van de intergraal de gem. temperatuur berekenen.
Ik moet de gem. temperatuur berekenen tussen 8 uur s'morgens en 6 uur s'avonds

intergraal:

24
̣(4sin(p(1-9)/12)+2)/(24-0)dt
0

-4cos(t-9/12*p)+2t
[-4*(12/p)*cos*(t-9/12)+2t]
maar hoe verder???

Wie kan mij hieer mee helpen
Alvast bedankt voor de moeite
Groetjes Mirella.....

Mirell
Student hbo - dinsdag 17 juni 2003

Antwoord

T(t) = 4 sin(p(t-9)/12)+2 Tekenen door gewoon wat waarden in te vullen:

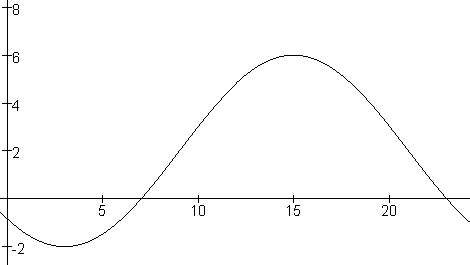
₀̣²⁴ 4·sin(p(t-9)/12)+2 = [-4·12/p·cos(p(t-9)/12) + 2t]₀²⁴
Noem die primitieve functie F(t), bereken nu: F(24)-F(0)= 48 (is totale oppervlakte "onder" de grafiek) en nu pas delen door 24 levert op 2 (de gemiddelde temperatuur over de hele dag).
Tussen 8 uur 's morgens en 6 uur 's avonds bereken je F(18)-F(8) vervolgens deel je dit dan nog door 10.

Met vriendelijke groet

JaDeX

dinsdag 17 juni 2003

©2001-2024 WisFaq