Re: Re: Hoe de primitive van e-machten vinden?

Dit is een reactie op vraag 12478

Hoi Wl,

Bedankt ik snap het, dit vroeg ik aan u om weer verder te kunnen met mijn som, maar het volgende snap ik niet:

geg: f(x)= e^-1 en g(x)= 2 met allebei R$\to$R
V is het vlakdeel ingesloten door de grafieken van f, g, en de y-as.
gevr:A) teken in een figuur de grafieken van g en bepaal de coordinaten van het snijpunt.

b) Bereken de oppervlakte van V

c) Bereken de inhoud van het lichaam dat ontstaat door V te wentelen om de x-as.

Mijn oplossing:

a) het snijpunt is x=1+ln2 y=2

b) dan komen de problemen: f(x)=e^-1 F=e^-1, en $\to$

g(x)= 2 , G(x)= 2x op dat interval [o,1+ln2] is g(x)$>$f(x)

dus men moet dit oplossen: integraalteken interval 0 tot met 1+ln2 G(x) - F(x) $\to$

G(x)$\to$ 2^(1+ln2)-1= 1,69 (ongev)
F(x)$\to$ 2-e^-1 = 1,63 (ongev) aftrekken levert 0,06 dus FOUT ! Maar hoe moet het dan wel ?

C) dit snap ik ook niet want de formule is:
$\pi$integraalteken f(x)²dx maar hier heb ik twee functies hoe berekend men de inhoud dan ?

Ik hoop dat u me (weer) kan helpen, het examen is overmorgen...

Shahra
Leerling bovenbouw havo-vwo - maandag 16 juni 2003

Antwoord

Hallo Shahram,

Ik ga er van uit dat f(x)=e^x-1

a) klopt



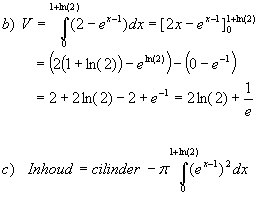
Grafiek g wentelen om de x-as geeft een cilinder met straal grondvlak = 2 en hoogte = 1 + ln(2)

Succes met je examen,

wl
maandag 16 juni 2003

Re: Re: Re: Hoe de primitive van e-machten vinden?

©2001-2024 WisFaq