Sinus, cosinus en tangens

Hoe zie ik wanneer ik cos, sin of tan moet gebruiken bij een driehoek?

tom gi
Overige TSO-BSO - maandag 9 juni 2003

Antwoord

Beste Tom,

Je hebt verschillende driehoeken: ongelijkzijdige driehoeken, gelijkbenige driehoeken, gelijkzijdige driehoeken, scherpe driehoeken, rechthoekige driehoeken en stompe driehoeken. De 'basisregels' van sinus, cosinus en tangens gelden in rechthoekige driehoeken.
Met 'basisregels' bedoel ik:

$
\eqalign{
& {\rm{sin = }}{{{\rm{Overstaande}}\,\,{\rm{rechthoekszijde}}} \over {{\rm{Schuine}}\,\,{\rm{zijde}}}} \cr

& {\rm{cos = }}{{{\rm{Aanliggende}}\,\,{\rm{rechthoekszijde}}} \over {{\rm{Schuine}}\,\,{\rm{zijde}}}} \cr

& {\rm{tan = }}{{{\rm{Overstaande}}\,\,{\rm{rechthoekszijde}}} \over {{\rm{Aanliggende}}\,\,{\rm{rechthoekszijde}}}} \cr}
$
Wat kun je nu met deze formules?

Twee dingen:

• je kunt als je één bepaalde hoek weet (de hoek van 90° mag niet genomen worden, altijd de scherpe hoek nemen) en de lengte van een bepaalde zijde, dan kun je m.b.v. een geschikte formule de andere zijde uitrekenen.
  
• Of als je de hoek wilt berekenen en je weet 2 zijden.
  

Je moet eerst weten wat de overstaande-, aanliggende- en schuine zijde is. In een rechthoekige driehoek is er uiteraard één rechte hoek, die hoek wordt ingesloten door twee zijden die overstaande rechthoekszijde en aanliggende rechthoekszijde worden genoemd, en er is één schuine zijde (de zijde die géén rechte hoek insluit). Het hangt ervan af welke hoek je neemt of gegeven krijgt welke zijde de overstaande- of aanliggende rechthoekszijde is. In onderstaand voorbeeld is de hoek $\alpha$ = $\angle$ABC. De rechte hoek wordt gevormd door de benen CA en AB. Omdat AB de hoek $\alpha$ mede insluit ($\alpha$ wordt namelijk ingesloten door AB en CB) wordt deze zijde de aanliggende rechthoekszijde genoemd. De andere zijde die de hoek van 90° insluit wordt overstaande rechthoekszijde genoemd (want deze sluit $\alpha$ niet in). De zijde die overblijft is de schuine zijde CB (dit is de enige zijde die de rechte hoek niet insluit; je kunt ook zeggen dat deze zijde de andere zijde is die de hoek $\alpha$ insluit en aanliggende is al bekend, overstaande kan niet dus blijft schuine zijde over).


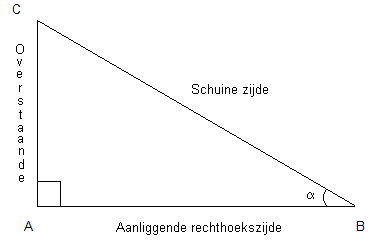
Het hangt er van af welke formule je gaat gebruiken. Het ligt er maar aan welke zijden bekend zijn, óf welke hoek(en) er gegeven is (zijn).

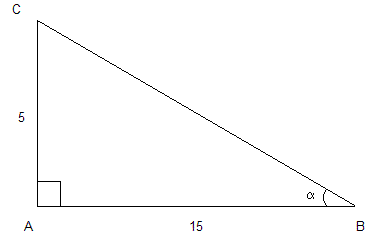
Stel dat je $\alpha$ wilt berekenen. Hoe ga je te werk? Er zijn 2 zijden bekend, namelijk de overstaande zijde (= 5) en de aanliggende zijde (= 15). Welke formule ga je gebruiken? Eentje waar overstaande- én aanliggende zijde in zit, dus de tangens. Tan($\alpha$) = ^AC/_AB = ⁵/₁₅ = ¹/₃.
Hoeveel graden is dat nu? Daarvoor moet je de inverse tangens nemen (op rekenmachine zal iets staan als tan^-1 of inv tan), als je dat doet kom je uit op 18,43...°. Je kunt ook als je de hoek weet de bijbehorende onbekende zijde berekenen (als je wist dat $\alpha$ = 18,43...° en je had alleen de overstaande óf aanliggende zijde gegeven, kon je met tangens de onbekende zijde berekenen).

Groetjes,

Davy.

Zie vraag 742

maandag 9 juni 2003

Re: Cos, sin, tan

Re: Cos, sin, tan

©2001-2024 WisFaq