Rotatie in een 3D ruimte

Je hebt een richtingsvector (A,B,C) (die de normaal voorstelt op het vlak Ax + By +Cz + D =0) en een rotatie as met richtingsvector (k,l,m) en door het punt (u,v,w). Hoe kun je het eenvoudigst de nieuwe richtingsvectoren (A',B',C') na rotatie over een bepaalde hoek rond de rotatie-as berekenen?

Olivie
Iets anders - dinsdag 3 juni 2003

Antwoord

Je hebt dus een rotatie-as r met puntvector (u,v,w) en richtingsvector (k,l,m)

De normaalvector (a,b,c) van je vlak mogen we ook door de oorsprong denken. Het gaat immers alleen om de richting ervan.

Misschien zijn er kortere methodes, maar volgens mij is het toch een heel recept.

1. transleer de rotatie-as r over (-u,-v,-w) zodat deze door de oorsprong loopt.
Echter, we moeten dan ook de normaalvector transleren. Daartoe transleren we 2 punten die op deze normaalvector liggen, te weten O en P(a,b,c)
O'(-u,-v,-w)
P'(a-u,b-v,c-w)

2. Roteer r zodanig dat deze parallel aan de z-as komt te liggen. Deze rotatiematrix noemen we A.
er moet gelden dat Ar=(0,0,1)^T
(T betekent getransponeerd, betekent (0,0,1) als kolommetje lezen ipv als rijtje)

Dit is hetzelfde als dat moet gelden:
A.(k,l,m)^T=(0,0,1)^T

Maar dan moeten we O' en P' eveneens volgens A transformeren:
O"=A.O'
P"=A.P'

3. Roteer O" en P" om de z-as volgens



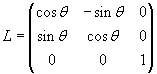
4. Transformeer O" en P" terug over A^-1
(Dit is de inverse matrix)

5. transleer de hele hap terug over (+u,+v,+w)^T

Het verschil tussen de 2 punten die je uiteindelijk hebt, vormt de normaalvector van het vlak na rotatie om de rotatie-as r.

groeten,
martijn

mg
donderdag 5 juni 2003

Re: Rotatie in een 3D ruimte

©2001-2024 WisFaq