Nat oppervlak van een gedeeltelijk gevulde horizontale cilinder

Ik zou graag willen weten hoe je het oppervlak van het gedeelte van de cilinder dat in contact staat met de vloeistof moet uitrekenen.

S. Arn
Student hbo - dinsdag 27 mei 2003

Antwoord

Ik neem aan dat je een horizontale cilinder bedoelt?



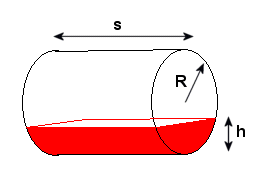
Hierboven de situatieschets.
Eerst gaan we het oppervlak van het gekromde gedeelte van de tankwand uitrekenen.
Daartoe bekijken we de tank van de voorkant (en we kantelen em een kwartslag, zoals je aan de kleur kunt zien):



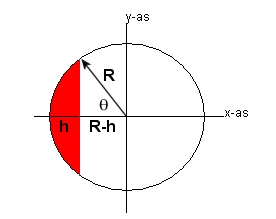
De voorkant is een cirkel met straal R:
y=√(R²-x²)
ter plaatse x=R-h, is
y=√(R²-(R-h)²)=√(2Rh-h²)
Nu willen we hoek $\theta$ weten. Omdat tan$\theta$=y/x, geldt dat
$\theta$=arctan(y/x)=arctan(√(2Rh-h²)/(R-h))

werken we in radialen, dan is de volle omtrek van de cirkel 2$\pi$R, en de cirkelboog die onder water staat dus
l=(2$\theta$/2$\pi$).2$\pi$R = 2$\theta$R
(2$\theta$ omdat de hoek van +$\theta$ naar -$\theta$ gaat)

Zou je het gedeelte dat onder water staat dus uitknippen uit de cilinder, dan zou je dat (na gladstrijken) een plaat opleveren in de vorm van een rechthoek, met
lengte=s en breedte=2$\theta$R
Zodoende weet je het oppervlak van het gekromde gedeelte van de tank.

Nu nog de kopse kanten. Dit is in feite het 2e plaatje het gedeelte dat rood gearceerd is. En dat maal 2 omdat je zo'n kopse kant aan weerszijden van de tank hebt.

Het oppervlak van het rode gedeelte is gelijk aan de taartpunt uit de cirkel die loopt van $\theta$ naar -$\theta$, en dan minus 2 keer het rechthoekige driehoekje gevormd door R en R-h.
O= (2$\theta$/2$\pi$).{opp.cirkel} - 2.(¹/₂basis.hoogte)
= (2$\theta$/2$\pi$).$\pi$R²-2.¹/₂.(R-h).√(2Rh-h²)
= $\theta$R²-(R-h).√(2Rh-h²)

de totale oppervlakte van de cilinder onder het vloeistofoppervlak is dus
2s$\theta$R + 2.($\theta$R²-(R-h).√(2Rh-h²))

groeten,
martijn

mg
woensdag 28 mei 2003

Re: Nat oppervlak van een gedeeltelijk gevulde horizontale cilinder

©2001-2024 WisFaq