Harmonische trilling

Bij de harmonische trilling van een punt is de uitwijking gegeven door u=1+2Cos2t. De vraag is voor welke waarden van t op [0,6] gaat het trillende punt door de evenwichtsstand heen. Ik begrijp dat Cos2t dan 0 moet zijn, want dan gaat de trilling door de evenwichtsstand, maar wat moet ik dan doen? Mijn antwoordenboekje komt dan ineens met 2t=0,5p en gaat dan verder met nog meer oplossingen, maar ik begrijp die stap niet. Kunnen jullie me helpen? Alvast bedankt.

Bram J
Leerling bovenbouw havo-vwo - zondag 25 mei 2003

Antwoord

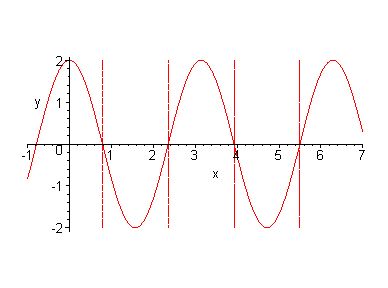
De uitwijking : y= 1+ 2*cos(2*x)

Die één verandert niet aan de evenwichtstoestand. Dus neem als nieuwe vergelijking:

y=2*cos(2*x) en dit moet 0 zijn. Dus:

cos(2*x)=0

De cosinus is nul als zijn argument een oneven veelvous is van p/2 Dus 2*x=(2k+1)*p/2 of x=(2k+1)*p/4 met kÎ
Je kiest dus natuurlijke getallen voor k zodat x binnen het interval [0,6] blijft.

De resultaten:

x=p/4 (k=0)
x=3*p/4 (k=1)
x=5*p/4 (k=2)
x=7*p/4 (k=3)

Hier grafisch:



Succes,

Koen Mahieu

zondag 25 mei 2003

©2001-2024 WisFaq