Re: Re: Rente in een meetkundige rij

Dit is een reactie op vraag 11466

Davy,
Ik mis 1 ding. Er wordt maandelijks € 250,- ingelegd. Deze berekening is eenmalig.
Tim

Tim
Student hbo - donderdag 22 mei 2003

Antwoord

Hoi,

Ja, klopt... ik was te snel geweest met antwoorden.
Je hebt niet gezegd dat de rente vast moest liggen, dus het rentepercentage is in 't begin hoog en wordt naarmate de maanden voorbijgaan steeds lager.
Ik heb de volgende berekening gemaakt. Indien je geen rente zou krijgen, dan had je na 36 maanden (elke maand 250€ gestort) 36·250€ = 9000€. Maar je hebt 10769,22€ op de bank staan, dus de totaal uitgekeerde rente is 10769,22€ - 9000€ = 1769,22€. Dus gemiddeld krijg je per maand 1769,22€ : 36 = 49,145€. Het rentepercentage is dan te berekenen in vergelijking met datgene wat je al op de bank hebt staan. Voor de eerste maand stort je 250€, gemiddeld krijg je daarop 49,145€ dus 49,145/250 = 0,197 en dat is 19,7% dus heb je na een maand je gestorte geld 250€ + je rente, dus 250 + 250·0,197 = 299,1€. De volgende maand begin je weer die 299,1€ maar stort jezelf weer 250€ erop waardoor je 549,1€ hebt. Je krijgt gemiddeld 49,145€ rente, dus 49,145/549,1 = 8,9% enz...

Ik heb er een Excel-bestand van gemaakt en na 36 maanden kwam er 10769,22€ als uitkomst. Maar of je dit bedoelde weet ik niet (want wordt er wel op de rekening met gekapitaliseerde rente gewerkt en mag de rente fluctueren?).

In het Excel-bestand vind je in kolom A het bedrag waarop de rente wordt berekend, in kolom B vind je het rentepercentage en in kolom C zie je het 'nieuwe' bedrag nadat de rente erbij opgeteld is. De rijen stellen de maanden voor.

P.S. Van mede-beantwoorder Tom heb ik de formule gekregen om via het eindbedrag, de maandelijkse storting en het totaal aantal maandelijkse stortingen een percentage te berekenen waarvoor geldt dat er elke maand een vast percentage wordt berekend.

De volgende formule is namelijk van toepassing

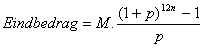
Hierin is M het bedrag dat je maandelijks stort, n het aantal jaren (je kunt 12n ook direct vervangen door het aantal maanden aangezien M ook in maanden is), en p is de maandelijkse rentevoet.

Via jouw gegevens: Eindbedrag = 10769,22 EUR hebben, is je M = 250, en 12n kan vervangen worden door 36.
Om daar je p uit te halen is geen pretje, maar via 'n slim softwarepakket (Maple) werd te achterhalen dat p = 1,000000207% (per maand).
Controle via Excel ondersteunt Maple.

En dankzij Hans Klein (weer 'n andere WisFaq'er) is er nog een berekening mogelijk:

Om meer informatie over de som van een meetkundige rij te krijgen kun je bijvoorbeeld kijken op deze pagina onder aan die pagina staat een interessante formule a*[(rⁿ-1)/(r - 1)].
Deze kunnen we ook gebruiken! a = begingetal = 250, r is de reden en nu nog onbekend, n is 36 en de som moet gelijk zijn aan 10769,22. Dus 250*[(x³⁶-1)/(x - 1)] = 10769,22. Laten we beide leden delen door 250.
(x³⁶-1)/(x - 1) = 10769,22/250 en dit is op te lossen door het linkerlid in je grafische rekenmachine te zetten, en het rechterlid in je grafische rekenmachine zetten, beide functies te plotten en het snijpunt bepalen.

Groetjes,

Davy.

donderdag 22 mei 2003

©2001-2024 WisFaq