Formule opstellen lineair verband

Kan iemand misschien uitleggen hoe je een linear verband opstelt?

shelle
Leerling bovenbouw havo-vwo - zondag 17 november 2002

Antwoord

De algemene formule voor een lineair verband is y = a·x + b. Dus de opdracht wordt: Zoek de getallen a en b.

a is het hellingsgetal of richtingscoëfficient.
Deze kun je vinden door de verandering van y te delen door de verandering van x.

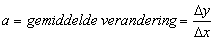
(0,b) is het snijpunt met de y-as. Dus b kun je vinden als je kijkt naar de waarde van y als x = 0. Je kunt b ook vinden door een punt van de grafiek in te vullen.

Voorbeeld
Wat is de formule van de lijn door A(2,6) en B(1,7)?

Uitwerking
We bereken eerst de richtingscoëfficiënt:



We zien a=-1. De vergelijking wordt y=-1·x+b.
We vullen de coördinaten van A in (B kan ook):

6=-1·2+b

Je krijgt dan een vergelijking waarin je alleen de waarde van b niet kent. Die vergelijking los je op:

6=-1·2+b
6=-2+b
b=8

De vergelijking van de gevraagde lijn is:

y=-x+8

Werkt de methode uit het voorbeeld altijd?
De bovenstaande methode met de vergelijkin werkt altijd. Met één uitzondering! Als de punten op een verticale lijn liggen. De toename van x zou dan nul zijn en delen door nul gaat niet... Toch kan je dan ook een formule geven voor de lijn. Het wordt iets als x=...

Voorbeeld
Geef de formule van de lijn door A(3,-1) en B(3,11).

Uitwerking
De punten A(3,-1) en B(3,11) liggen op een verticale lijn. De vergelijking wordt: x=3.

P.S.
Het voorbeeld hierboven kon je natuurlijk veel handiger doen. Als je de punten tekent zie je meteen dat de richtingscoëfficiënt gelijk is aan -1. (Eén eenheid naar rechts... één eenheid omlaag!). Als je bij x=1 op y=7 bent en de richtingscoëfficiënt is -1, dan snijdt de lijn de y-as in het punt (0,8). Dus de vergelijing is: y=-x+8. Maar meestal gaat dat niet zo makkelijk en de bovenstaande werkt altijd... (nou ja bijna altijd!)

zondag 17 november 2002

©2001-2024 WisFaq