Re: Kwadratuur van rechthoek en driehoek
Wat is het bewijs dat de oppervlakte van de driehoek, evengroot is als de oppervlakte van het vierkant bij deze vraag. Dus hoe kun je het bewijzen. Zouden jullie het hele bewijs kunnen opschrijven voor me, want zelf kom ik er niet uit...
Maarte
Leerling bovenbouw havo-vwo - vrijdag 9 mei 2003
Antwoord
Zoals zo treffend uitgedrukt op Kwadratuur van een driehoek gaat om de volgende situatie:
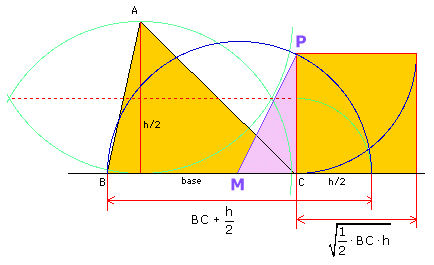
Opp($\Delta$ABC)=1/2·BC·h
In $\Delta$MCP geldt:
MP=1/2·BC+h/4
MC=1/2·BC-h/4 (ga na!)
Dus:
CP2=(1/2·BC+h/4)2-(1/2·BC-h/4)2
CP2=1/4BC2+BC·h/4+h2/16-1/4BC2+BC·h/4-h2/16
CP2=BC·h/2=1/2·BC·h
Dus: Opp($\Delta$ABC)=Opp(vierkant) Q.E.D.
vrijdag 9 mei 2003
©2001-2024 WisFaq
|
Dit is een reactie op vraag 1987