Differentiëren

Als je van een functie de 2e afgeleide moet berekenen, reken je eerst de 1e afgeleide uit, maar vaak is deze dan zo ingewikkeld dat je het jezelf alleen maar moeilijker maakt. Hoe hou je overzicht en kun je het jezelf makkelijker maken?
bv bij:
(8x³-24x)/(x²+1)³

Kim
Leerling bovenbouw havo-vwo - woensdag 7 mei 2003

Antwoord

De functie die je geeft vind ik nu niet zo ingewikkeld, er staat maar 1 factor in de teller en 1 in de noemer.

Je moet wel bedenken dat, bijvoorbeeld van de functie die je opgeeft, hogere afgeleiden echt wel langer *worden*, dus op zich kan je daar niet veel aan doen. Maar misschien heb je hier iets aan...

Regel van Leibniz

Er bestaat een formule voor de n-de afgeleide van het produkt van twee functies (regel van Leibniz). Die kan je vooral bij hogere afgeleiden wat werk besparen.



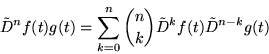
Ik zal even schetsen waarom die formule handig kan zijn. Stel we willen de derde afgeleide berekenen van een produkt van 2 functies. Normaal zou je dan zo te werk gaan

D[fg]
= f'g+fg'

D²[fg]
= D[D[fg]]
= D[f'g+fg']
= f"g+f'g'+f'g'+fg"

D³[fg] = D[D²[fg]]
= D[f"g+f'g'+f'g'+fg"]
= f'''g+f"g'+f"g'+f'g"+f"g'+f'g"+f'g"+fg'''

Twee van de termen in D²[fg] zijn gelijk, maar als je dat niet merkt en verder rekent, doe je eigenlijk werk dubbel. De regel van Leibniz houdt gewoon onmiddellijk rekening met het feit dat sommige van die termen gelijk zijn.

Regel van Wisfaq-Leibniz

Je kan de regel van Leibniz veralgemenen naar een produkt van m functies. Ik vermoed sterk dat een bewijs door volledige inductie van de volgende techniek eenvoudig is. Zelf heb ik die gevonden door te "kijken" en ik zal je hem aanbrengen in de vorm van een voorbeeld.

We willen de vierde (=n) afgeleide berekenen van een produkt van drie (=m) functies a, b en c.

Elke term in de uiteindelijke uitdrukking zal van de vorm a(i)b(j)c(k) zijn. Hierbij duiden de getallen tussen haakjes aan welke afgeleide je van de bewuste functie moet nemen, met de afspraak dat de nulde afgeleide overeenkomt met de functie zelf. Om de functies niet altijd bij naam te moeten schrijven stellen we bovenstaande vorm door [i,j,k].

Wat ook opvalt is dat voor elke [i,j,k] i+j+k=n. We moeten dus eerst alle combinaties [i,j,k]

noteren. Dat aantal is wat men noemt een "herhalingscombinatie" en wordt gegeven door N =

(n+m-1)!/[n!(m-1)!], dus in ons voorbeeld 15.

[4,0,0] [0,4,0] [0,0,4]
[3,1,0] [3,0,1] [0,3,1] [0,1,3] [1,0,3] [1,3,0]
[2,2,0] [2,0,2] [0,2,2]
[2,1,1] [1,2,1] [1,1,2]

Elk van die [i,j,k] moet vermenigvuldigd worden met een coefficient C die gegeven wordt door n!/(i!j!k!). Dus

[4,0,0] [0,4,0] [0,0,4] - C = 4!/4! = 1
[3,1,0] [3,0,1] [0,3,1] [0,1,3] [1,0,3] [1,3,0] - C = 4!/(3!1!) = 4
[2,2,0] [2,0,2] [0,2,2] - C = 4!/(2!2!) = 6
[2,1,1] [1,2,1] [1,1,2] - C = 4!/(2!1!1!) = 12

De vierde afgeleide van abc is dus

a''''bc + ab''''c + abc''''
+4{a'''b'c + a'''bc' + ab'''c' + ab'c''' + a'bc''' + a'b'''c}
+6{a''b''c + a''bc'' + ab''c''}
+12{a''bc + ab''c + abc''}

Nu ik de algemene techniek heb toegelicht, hier enkele eenvoudige voorbeelden die je van de correctheid moeten overtuigen.

Voorbeeld 1

m=2 en n=1 = N=2

[0,1] - C = 1!/1! = 1
[1,0] - C = 1!/1! = 1

D[ab] = a'b + ab'

Het resultaat is de gekende produktregel

Voorbeeld 2

m=2 en n willekeurig = N=n+1

[0,n] - C = n!/n! = 1
...
[i,n-i] - C = n!/[i!(n-i)!]
...
[n,0] - C = n!/n! = 1

Het resultaat is de regel van Leibniz voor de n-de afgeleide van het produkt van twee functies die we hierboven al gaven.

Voorbeeld 3

De functie die we willen afleiden mag ook rationaal zijn. Je moet dan wel niet de afgeleiden van de noemer kennen maar de afgeleiden van het omgekeerde van de noemer. Hier zou je de formule van Faa di Bruno kunnen gebruiken, maar daar zullen we maar niet verder op in gaan.

Wat is de derde afgeleide van de volgende functie?

f(x) = [(x³-2)(x-4)²]/[(x²-x)²]

a(x) = x³-2
a'(x) = 3x²
a"(x) = 6x
a'''(x) = 6

b(x) = (x-4)²
b'(x) = 2(x-4)
b"(x) = 2
b'''(x) = 0

c(x) = (x²-x)^-2
c'(x) = [-2(x²-x)^-3].[2x] = p(x).q(x)
c"(x) = p'(x)q(x) + q'(x)p(x)
c'''(x) = p"(x)q(x) + 2p'(x)q'(x) + p(x)q"(x)

m=3, n=3 = N=10

[3,0,0] [0,3,0] [0,0,3] - C = 3!/3! = 1
[2,1,0] [2,0,1] [0,1,2] [0,2,1] [1,0,2] [1,2,0] - C = 3!/[2!1!] = 3
[1,1,1] - C = 3!/[1!1!1!] = 6

Uiteindelijk vind je f''' als

a'''bc + ab'''c + abc'''
+3[a"b'c + a"bc' + ab'c" + ab"c' + a'bc" + a'b"c]
+6[a'b'c']

Aan het praktische gebruik bij rationale functies moet ik duidelijk nog wat werken :/ Het nut ervan is dan ook het grootst bij heel hoge afgeleiden en produkten van heel veel functies.

Wat je wel kan onthouden is dat je om het overzicht te bewaren er misschien goed aan doet eerst delen van de uitdrukking een naam te geven en symbolisch de gevraagde afgeleide te berekenen om dan daarna de afgeleiden van de delen in te vullen.

vrijdag 9 mei 2003

©2001-2024 WisFaq