Loodrechte snijlijnen

Als je een plot maakt van de grafieken van de functies f(x) = x² en g(x) = x⁴ in het interval (0, 1), hebben deze twee snijpunten. Daartussen loopt de grafiek van g constant onder die van f. Rond de lijn y = 1 - x lijkt een lijn te bestaan die BEIDE functies precies loodrecht snijdt? Bestaat deze lijn echt, en zo ja, waar ligt deze?

Ik heb al geprobeerd om gewoon te zeggen: hij ligt op y = ax + b en de x-coördinaten van de snijpunten zijn zodanig dat ax + b = x² en dat ax + b = x4. Je hebt om de richting van de gezochte lijn te bepalen twee punten nodig die respectievelijk aan de vergelijkingen voldoen, waarbij de afgeleiden f'(x) = 2x en g'(x) = 4x³ aan elkaar gelijk zijn, en die op een lijn liggen die beide grafieken ook daadwerkelijk LOODRECHT snijdt. Het is dus erg moeilijk om deze lijn te bepalen.

P.S. Natuurlijk bedoel ik niet de oplossing x = 0...

Erik L
Leerling bovenbouw havo-vwo - woensdag 7 mei 2003

Antwoord

Kies op de grafiek van g het punt A(a,a⁴).
De richtingscoëfficient(rico) van de raaklijn aan de grafiek
van g in dit punt is 4a³.
De gezochte lijn (k) staat in A loodrecht op deze raaklijn en heeft dus rico ^-1/_(4a³)=-0.25a^-3.
k heeft dus vergelijking y=-0.25a^-3·(x-a)+a⁴.
Dit schrijven we als
y=-0.25a^-3·x+0.25a^-2+a⁴.

Dit snijden met de parabool y=x² levert
x²+0.25a^-3·x-0.25a^-2-a⁴=0.

Oplossen met de abc-formule geeft: (we kiezen alleen de positieve oplossing):

x=(-0.25a^-3+Ö(0.0625a^-6+4(0.25a^-2+a⁴))/2

De raaklijn in dit punt van de parabool f heeft rico 2x, en dit moet gelijk zijn aan 4a³.

Dit levert
-0.25a^-3+Ö(0.0625a^-6+4(0.25a^-2+a⁴)=4a³

Deze vergelijking ziet er niet zo leuk uit, een benaderde oplossing met de GRM geeft a=.6409438968.

Dit invullen in de vergelijking van k geeft:
y=-0.949467185x+0.777319297

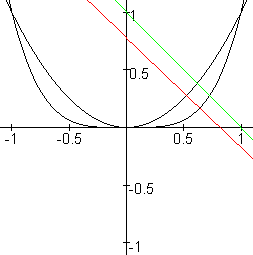
Hieronder een plaatje (de gezochte lijn in rood en de lijn y=1-x in groen)



Groet
hk

donderdag 8 mei 2003

©2001-2024 WisFaq