Bolstapeling en kegel

Ik heb de volgende vraag:
Als je 4 tennisballen verpakt in een kegel, wat is de inhoud daarvan? Is dit ook mogelijk met een halve bol (gewoon een bol in 2 snijden) en wat is daar de inhoud dan van. Alvast bedankt
Michiel

Michie
3de graad ASO - woensdag 7 mei 2003

Antwoord

Dat was niet eenvoudig. Ik dacht eigenlijk dat deze vraag al eerder beantwoord was, maar in de vorige vragen ging het om een viervlak, en niet om kegel of halve bol.
Eerst maar eens de kegel.
Ik vermoed dat je de kleinste inhoud krijgt (ik neem aan dat het gaat om de kegel met de kleinste inhoud) als je drie ballen op de grond legt, ieder elk ander rakend, en 1 erbovenop in het kuiltje, maar ik ben daar niet helemaal zeker van.
Vervolgens moet je een beschrijvende van de kegel vinden.
Die beschrijvende vind je in het volgende plaatje: een vlak door de middens van een van de grondballen en de bovenbal, en door het raakpunt van de andere twee grondballen.

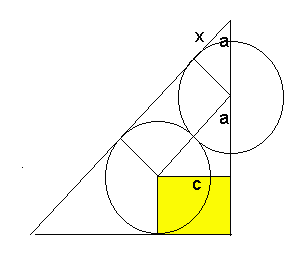
Hoeken die met a zijn aangeduid, zijn gelijk, omdat de beschrijvende evenwijdig is met de verbindingslijn van de middelpunten.
Noem de straal van de ballen 1.
De vier middelpunten van de ballen vormen een regelmatig viervlak, met zijde 2. De hoogte van dit viervlak is ²/₃Ö6.
Bekijk nu de rechthoekige driehoek in het midden van het plaatje. De horizontale zijde is c, de verticale zijde is de hoogte van het viervlak, en de schuine zijde is tweemaal de straal van de bal, dus 2.
Dan geldt: c=²/₃Ö3
(Pythagoras)
dus:
tan(a)=c/(hoogte viervlak)=(²/₃Ö3)/(²/₃Ö6)=¹/_Ö2
Maar ook: tan(a)=¹/_x
dus x=Ö2
De hoogte h van de kegel is dus: h=1+²/₃Ö6+Ö3
Om de straal r van het grondvlak van de kegel te berekenen, gaan we nog een keer de tangens gebruiken:
tan(a)=^r/_h=¹/_Ö2, dus r=^h/_Ö2
De inhoud van de kegel is dus ¹/₃pr²h, ofwel ¹/₆ph³.
Uitwerken levert: p(3+⁷/₃Ö3+⁴⁴/₂₇Ö6+2Ö2).

Bedenk wel: als de straal van de bal niet 1 is, maar R, dan moet de inhoud met R³ vermenigvuldigd worden.

Dan de halve bol.
Als je als straal van deze halve bol de hoogte neemt van het grondvlak tot de bovenkant van de bovenbal, dan raakt deze halve bol niet aan de drie grondballen. Deze halve bol is dan niet die met de kleinste inhoud.
Je kunt de bovenbal dan iets laten zakken, zodat de grondballen elkaar niet meer raken.
Nu nog berekenen hoever je de straal van de halve bol kunt inkrimpen, dus de bovenbal kunt laten zakken waardoor de grondballen uit elkaar gaan tot zij ook de halve bol aan de binnenkant raken.
Noem y de afstand die het middelpunt van de bovenbal zakt.
De straal van de halve bol is dan B=2+²/₃Ö6-y
De nieuwe c kun je dan uitdrukken in y met Pythagoras:
c = Ö(4-(²/₃Ö6-y)²)
De straal B is dan ook gelijk aan de diagonaal in de gele rechthoek plus 1.
Nog een keer Pythagoras voor de diagonaal in de gele rechthoek: Ö(⁷/₃+⁴/₃yÖ6-y²)
De twee uitdrukkingen voor B gelijkstellen levert
y = ²/₃Ö6 - 1.
dus B = 3.
Achteraf wel logisch eigenlijk, want je kunt zeven cirkels met straal 1 kwijt in een cirkel met straal 3.

In onderstaande Cabri kun je het middelpunt van de bovenbal verschuiven totdat de halve bol beide ballen raakt.



De inhoud van de halve bol is dan 18p.

groet,

woensdag 21 mei 2003

©2001-2024 WisFaq