\require{AMSmath}

Ptolemeus en de ontwikkeling van de goniometrie

Hallo, ik zit in 5VWO en moet een p.o. maken over goniometrie. Een van de vragen die ik in mijn p.o. moet beantwoorden is, dat ik diverse goniometrische formules die Ptolemeus nodig heeft gehad en die hij zelf heeft ontworpen, moet onderzoeken en deze formules moet ik ook afleiden. Nu heb ik bergen van informatie over Ptolemeus gevonden, maar niet de informatie over de formules die ik zocht. Ik hoop dat u me kunt helpen met deze vraag en alvast één van de formules voor mij kunt afleiden.

Joyce
Leerling bovenbouw havo-vwo - donderdag 10 april 2003

Antwoord

Ik citeer uit een standaard werk over de geschiedenis van de wiskunde (Histoy of Mathematics van D.E. Smith):

"The original contributions of Ptolemy (c. 150) to trigonometry are few, if any; but we are greatly indebted to him for his summary, in the Almagest, of the theorems known to Hipparchus" (pag. 607).

En verder (p. 615):

"The third important table of chords is that of Ptolemy. He divided the circle into 360° and the diameter into 120 equal parts (...). Influenced like Hipparchus by Baylonian precendents, he used sexagesimal fractions (...)."

Die koordentabellen waren nodig voor zijn astronomische berekeningen.

En tenslotte (p.630):

"The important relation now expressed as
a/sin(A) = b/sin(B) = c/sin(C)
was known to Ptolemy in substance, although he expressed it by means of chords".

In de Almagest (boek I) wordt de koordentabel beschreven.
P. leidt daarbij eerst de waarden voor sin 18° en sin 36° af (op basis van de gulden snede, zoals beschreven in de Elementen van Euclides).
Hij noemt de waarden niet, maar drukt ze uit in termen van de delen van de middellijn van de cirkel met die hoeken als omtrekshoek).



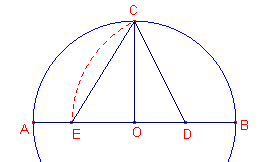
Op basis van bovenstaande figuur toont P. aan, dat BO de zijde is van een regelmatige zeshoek, en EO die van een regelmatige 10-hoek, en ook
(zijde vijfhoek)²=(zijde zeshoek)²+(zijde 10-hoek)² = CO² + OE² = EC²
Hij stelt nu DO = 30, DO² = 900, OC = 60, OC² = 3600
Zodat DE² = DC² = 4500.
En hij vindt: DE = 67|4|55 (met de betekenis 67 + 4/60 + 55/3600).
Daarom is de zijde van de 10-hoek: koorde(36°) = DE - DO = 37|4|55.
Enzovoorts.

Dan nu maar Ptolemaeus' stelling (die als tweede eigenschap in boek I voorkomt):
Voor een in een cirkel beschreven vierhoek ABCD met diagonalen AC en BD geldt:
AC.BD = AB.CD + AD.BC
In de Almagest komt hetzelfde bewijs van de stelling voor als te vinden is op onderstaande webpagina.
Deze stelling wordt door P. als hulpstelling gebruikt bij z'n verdere koorde-berekeningen.

Bekijk nu de onderstaande figuur (en we volgen Ptolemaeus min of meer - in vertaling):



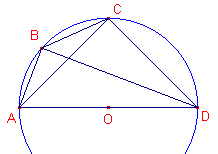
Laat nu AB, BC twee bogen zijn eindigend in A, het einde de diameter AD van een cirkel.
En laat AC (=A) groter zijn dan AB (=B).
Onderstel nu dat koorde(AC) en koorde(AB) gegeven zijn: dan wordt geëist koorde(BC) te berekenen.
Teken BD en CD.
Dan is: AC.BD = BC.AD+AB.CD
Nu zijn AB en AC gegeven; dus zijn BD = koorde(180-AB) en CD = koorde(180-AC) bekend. En AD is bekend. De overblijvende koorde BC is bekend.

We vinden dan in P.'s terminologie (k staat voor koorde):
k(A-B).k(180) = k(A).k(180-B) - k(B).k(180-A)

En dit is wat we hedentendage schrijven als
sin(P-Q) = sin(P).cos(Q) - cos(P).sin(Q)
waarbij A = 2P en B = 2Q.

Met deze formule vond Ptolemaeus:
koorde(12°) = koorde(72°-60°) = 12|32|36

Ik hoop dat je vraag hiermee naar genoegen is beantwoord. En vergeet niet de bronvermelding (WisFaq) op te nemen in je PO, als je het bovenstaande gebruikt!!

Zie Stelling van Ptolemaeus

dk
donderdag 10 april 2003

©2001-2024 WisFaq