Ook al is een dergelijke vraag al eens eerder beantwoord, we doen het nog maar eens (motto: herhaling is de kracht van het onderwijs).
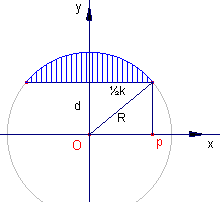
In bovenstaand plaatje is d de afstand van O tot de koorde.
Als het plaatje een zijkant weergeeft van een horizontaal gelegen tank, die tot aan de koorde gevuld is (met een vloeistof), dan kunnen we wel enkele berekeningen maken. Uit de (door de vragensteller gezonden extra) gegevens blijkt, dat de inhoud van de volle tank gelijk is aan 5270 dm3.
De oppervlakte van de cirkel is 3.14 x 6,35 x 6,35 = 126,6 dm2.
De lengte b van de tank is dan 5270 / 126,6 = 41,6 dm.
Om echter de vulling van de tank te berekenen (dus de hoeveelheid tot aan de koorde) hebben we nog een gegeven nodig: bijvoorbeeld de afstand h van de bovenkant van de tank tot aan het vloeistofoppervlak te meten met een peilstok).
Dan is d = R - h.
Met de stelling van Pythagoras kan dan de lengte van de koorde worden berekend.
Daarvoor geldt:
k = 2 (R2-d2)
(R2-d2)
Voor de oppervlakte A van het gedeelte boven de koorde (het cirkelsegment, het lege deel van de tank) geldt:
A = R2arcsin( k /(2R) ) - 1/2kd
De variabelen (R, k, d) in het rechter lid zijn nu bekend.
A dus ook.
De inhoud I van de het lege deel van de tank is dan I = A.b, zodat we de inhoud van de "vulling" gemakkelijk kunnen vinden.
Zie Formules
dk
zondag 17 november 2002

