Voor punt B krijg ik dan: B(x,y)= T(x,y) + ( 2·cos( f ·t), 2·sin( f ·t)) Parametervoorstelling B is dan:
x = 6cos (( p /4) ·t) + 2· cos ( p ·t)
y = 6sin (( p /4) ·t) + 2· sin ( p ·t)
Dan vul je deze in je grafische rekenmachine in. Dan krijg ik een heel rare beweging die toch volgens mij wel zou kunnen. Maar deze is heel anders dan de twee plaatjes die u gegeven hebt. Maar volgens mij zijn dit de bewegingen die de bakjes maken aan de arm. Daarom weet ik niet of die plaatjes van mij kloppen.
De snelheid is het grootst als de bakjes en de arm dezelfde kant op bewegen.
Dit kan ik bereken door eerst de baansnelheid te berekenen. Dit doe je met de formule:
v = Ö ((dx/dt)2+(dy/dt)2)
(dx/dt) = -6sin(.25 p ·t) · .25 p + -2 sin( p ·t) · p
(dy/dt) = 6 cos (.25 p ·t) · .25 p + 2 cos( p ·t) · p
(dx/dt)2 = (-6sin(.25 p ·t) · .25 p + -2 sin( p ·t) · p )2
(dy/dt)2 = (6 cos (.25 p ·t) · .25 p + 2 cos( p ·t) · p )2
En dit dan natuurlijk verder uitschrijven:
v=Ö((-6sin(.25p·t)·.25p+-2sin(p·t)·p)2)+(6cos(.25p·t)·.25p+2cos(p·t)·p)2)
Dit dan in je rekenmachine zetten. Je krijgt dan een soort sinusoïde, maar eigenlijk niet. Het patroon herhaalt zich na 14 t. Je kan uit de grafiekaflezen dat bij t = 14,6667 de snelheid minimaal is. De snelheid is dan 1,57079. Dit kan je ook met je rekenmachine bepalen met minimum en maximum.
Er is een maximum bij t = 15,99999 en de hoogte is 10,995574. Als de snelheid maximaal is bewegen de arm en de bakjes dezelfde kant op. De snelheid is minimaal als het bakje en de arm in tegenovergestelde richting draaien.
E.T.
Leerling bovenbouw havo-vwo - maandag 4 maart 2002
Volgens mij is dit (bijna) allemaal goed! De parametervoorstelling, die je gemaakt hebt, is dezelfde als die ik gebruikt heb voor de plaatjes bij de vorige vraag. Misschien werkt het op je GR iets anders... misschien moet je het 'domein' van t apart opgeven... en het scherm natuurlijk aanpassen zodat het er op past.Maar wat je hebt opgeschreven is, volgens mij, goed en dat is mooi. Alleen het stukje met die 14t begrijp ik niet helemaal!
Als ik die laatste v=... uitwerk (nou ja met Derive...:-) dan krijg ik deze snelheidsfunctie:
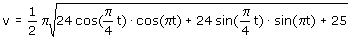
(Dat is NIET nodig, want je kunt 'm ook zonder uitwerken in je GR zetten!)
Even tekenen!?
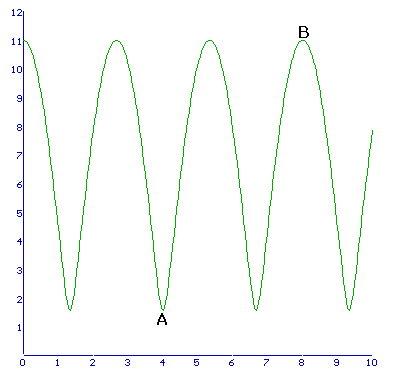
..en inderdaad de snelheid is het hoogst na 22/3, 51/3 en 8 seconden... dus dat klopt wel. Bij het invoeren in je GR moet je dus ook nog even goed uitkijken dat je het goed invoert... en dat maximum is natuurlijk 'gewoon' bij t=16 toch? Een paar interessante punten: Een minimum bij t=4 (A) en een maximum bij t=8 (B).
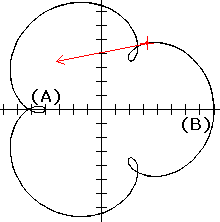
Zie vraag 1816
WvR
dinsdag 5 maart 2002

