Uitslag afgeknotte kegel

Hoe kan ik een uitslag maken van een afgeknotte kegel?
Driedimensionaal heb ik een kap, hoogte 800 mm, bovendiameter 514, onderdiameter 800 mm.

• Hoe ziet de vorm eruit als ik die plat uitvouw?
• Hoe kan ik dat tekenen/berekenen?

m.wijn
Docent - donderdag 21 februari 2002

Antwoord

Eerst maar eens een tekening:



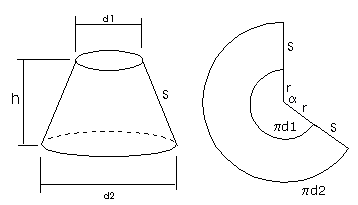
$s$ kan je uitrekenen met de stelling van Pythagoras.



$
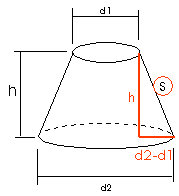
\eqalign{s = \sqrt {\left( {\frac{{d_2 - d_1 }}
{2}} \right)^2 + h^2 }}
$

De grote vraag hier is natuurlijk wat is r en wat is $\alpha$?

$r$ reken je uit met gelijkvormigheid en verhoudingen:



$
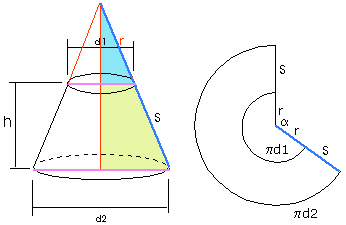
\eqalign{\frac{{r + s}}
{{d_2 }} = \frac{r}
{{d_1 }}}
$

$\alpha$ reken je uit als volgt:

$
\eqalign{\alpha = 360^o \cdot \left( {1 - \frac{{d_1 }}
{{2r}}} \right)}
$

Voorbeeld

$
\eqalign{
& d_1 = 3 \cr
& d_2 = 5 \cr
& h = 6 \cr
& s = \sqrt {\left( {\frac{{5 - 3}}
{2}} \right)^2 + 6^2 } = \sqrt {37} \cr
& \frac{{r + \sqrt {37} }}
{5} = \frac{r}
{3} \Rightarrow r = 1\frac{1}
{2}\sqrt {37} \cr
& \alpha = 360^\circ \cdot \left( {1 - \frac{3}
{{2 \cdot 1\frac{1}
{2}\sqrt {37} }}} \right) \approx 301^\circ \cr}
$

Antwoord op de vraag

h=800
d₁=514
d₂=800

$
\eqalign{
& s = \sqrt {\left( {\frac{{800 - 514}}
{2}} \right)^2 + 800^2 } \approx 812,7 \cr
& \frac{{r + 812,7}}
{{800}} = \frac{r}
{{514}} \Rightarrow r \approx 1460,6 \cr
& \alpha = 360^o \cdot \left( {1 - \frac{{514}}
{{2 \cdot 1460,6}}} \right) \approx 297^o \cr}
$

Zie ook Re: Uitslag afgeknotte kegel

Vragen naar aanleiding van dit antwoord? Klik rechts..! donderdag 21 februari 2002

©2004-2024 WisFaq