\require{AMSmath}

Krommen in de ruimte

Hey iedereen, ik heb een probleemke,
Ik moet voor mijn eindwerk vergelijkingen opstellen van 3 verschillende kegelsnedes. In de ruimte, met x, y en z dus.
Mijn kegelsnedes zijn: -2 cilinders onder 90°
-2 cilinders onder 45°
-een cilinder en een kegel onder 90°
De snedes die je krijgt zijn geen ellipsen, cirkels,... Eerder eivormen. Ik hoop dat iemand mij kan helpen want zelfs mijn wiskunde leerkracht heeft het er moeilijk mee.

Joke
3de graad ASO - woensdag 23 april 2003

Antwoord

Daar zijn we weer! Ik heb inmiddels via-via wat plaatjes gekregen, dat is wel mooi!



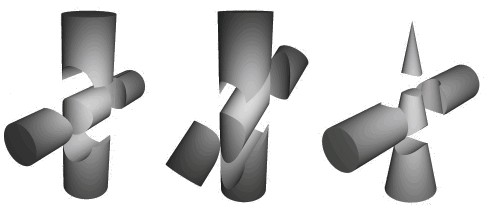
Blijft de vraag: Wat wil je nu precies uitrekenen?
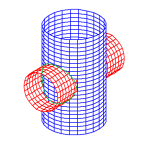Ik vermoed dat je een parametrisering van de kromme wilt weten die op steeds op beide cilinders of op de cilinder en de kegel ligt. Dus als voorbeeld:

x=3·sin(t)
y=3·cos(t)
z=u

en

x=v
y=2·sin(w)
z=2·cos(w)

De punten van die kromme liggen op beide cilinders, dus is nu even de vraag hoe je die twee p.'s kan combineren. Wel nu... de y en de z van de laatste zijn misschien wel handig... moeten we alleen x nog 'even' zo kiezen dat het klopt.

v=3·sin(t)

Als we v kunnen uitdrukken in w, dan zijn we er! Er geldt:
3·cos(t)=2·sin(w)
cos(t)=²/₃·sin(w)
t=arccos(²/₃·sin(w)) (en nog één voor de andere kromme!)
v=sin(arccos(²/₃·sin(w)))

Dus de kromme laat zich schrijven als:

x=sin(arccos(²/₃·sin(w)))
y=2·sin(w)
z=2·cos(w)

En dat laat zich dan schrijven als:

x=Ö(9-4·sin²w)
y=2·sin(w)
z=2·cos(w)

Is dit wat je bedoelt?

WvR
donderdag 1 mei 2003

©2001-2024 WisFaq