WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Extremumvraagstuk

Geachte,

Ik moet de volgende oefening op lossen:

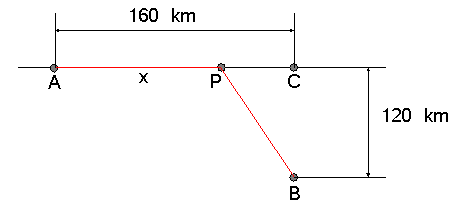
Er moet een aardolieleiding worden aangelegd van punt A langs de kust naar punt B 120 km landinwaarts. Omdat de aanlegkosten in het binnenland 5000€/km bedragen en langs de kust 3000€/km, is het raadzaam om de pijpleiding eerst een stuk langs de kustlijn te laten lopen naar een punt P.

Als je weet dat de afstand van A naar punt C 160km is, waar moet P dan gekozen worden zodat de aanlegkosten minimaal zijn? Wat zal de prijs zijn voor de hele installatie?

Ik heb al hetvolgende gevonden: C(x) = 3000 x + 5000 $\sqrt{}$((160-x)²+120²). Nu moet ik de afgeleide berekenen en die gelijkstellen aan 0, maar ik weeet niet zo goed hoe daaraan geraak.
Kan u mij verder helpen?

Alvast bedankt

Yosra
yosra
Student Hoger Onderwijs België - zaterdag 30 december 2023

Antwoord

Dat is mooi. Ik heb nog wel een extra paar haakjes gezet en als het goed is dan gaat het om de afgeleide van:

$
C\left( x \right) = 3000x + 5000\sqrt {\left( {160 - x} \right)^2 + 120{}^{^2 }}
$

Uitgewerkt krijg je:

$
\eqalign{
& C\left( x \right) = 3000x + 5000\sqrt {\left( {160 - x} \right)^2 + 14400} \cr
& C'(x) = 3000 + 5000 \cdot \frac{1}
{{2\sqrt {\left( {160 - x} \right)^2 + 14400} }} \cdot 2\left( {160 - x} \right) \cdot - 1 \cr
& C'(x) = 3000 - 5000 \cdot \frac{1}
{{\sqrt {\left( {160 - x} \right)^2 + 14400} }} \cdot \left( {160 - x} \right) \cr
& C'(x) = 3000 - 800000 \cdot \frac{1}
{{\sqrt {\left( {160 - x} \right)^2 + 14400} }} - 5000 \cdot \frac{{ - x}}
{{\sqrt {\left( {160 - x} \right)^2 + 14400} }} \cr
& C'(x) = 3000 + \frac{{5000x - 800000}}
{{\sqrt {\left( {160 - x} \right)^2 + 14400} }} \cr}
$

Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 30 december 2023