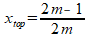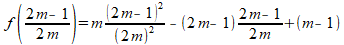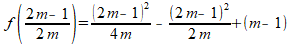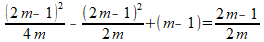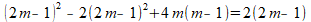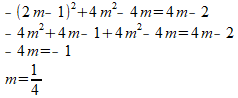WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Een vergelijking met 2 onbekenden

Hallo

Ik heb deze vraag al verschillende keren opgelost, maar vond steeds geen oplossing.

Beschouw de familie van functies fm: R$\Rightarrow$R gegeven door: fm(×)= mx²-(2m-1)x+(m-1) met m verschillend van nul.
Bepaal de waarde van m waarvoor de top van de grafiek op de eerste deellijn ligt.

Ik heb het volgende geprobeerd:

De top van de grafiek is T(-b/2a,f(-b/2a)) en -b/2a = (2m-1)/2m
De vergelijking van de eerste deellijn is x=y dus heb ik (2m-1)/2m = f((2m-1)/2m)
Ik kwam uit dat m = -7 is, terwijl de oplossing in het boek is dat m=1/4

Alvast bedankt
X
Leerling bovenbouw havo-vwo - zaterdag 3 juli 2021

Antwoord

Hallo mr. X,

Je gedachte is goed, dan is het alleen nog een kwestie van zorgvuldig invullen en uitwerken. Je had al gevonden:

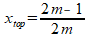
Dat levert voor de y-coördinaat van de top:

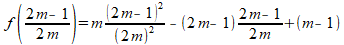
ofwel:

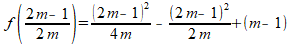
Je moet dus oplossen:

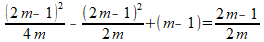
Even de gehele vergelijking vermenigvuldigen met 4m om de breuken kwijt te raken:

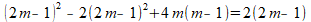
Tot slot netjes uitwerken:

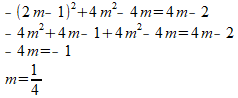
OK zo?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 3 juli 2021