WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlskte

Beste,

Zou u mij a.u.b. kunnen helpen? Het gaat om de volgende opgave als voorbeeld:

Gegeven is de parameterkromme K door: x(t) = -t²+ 6t en y(t)= -¹/₃t³+ 2t². Bereken de oppervlakte van het vlakdee dat geheel wordt ingesloten door K.

Het is geen probleem om de t-waarden te vinden bij het dubbelpunt en ook het meest rechtse punt van de kromme bij t=3.

Maar dan: de bovenkant loopt van t=6 tot t=3, want dan zou volgens de theorie de dx positief zijn. Kunt u mij dit uitleggen? Voor mij is dx de breedte van zo'n "klein rechthoekje" (dus altijd positief zou ik denken)

Voor de onderkant loopt t van 0 naar 3 (dus dx ook positief??) Blijkbaar is de richting van de baan cruciaal om dx positief of negatief te laten zijn, maar ik snap dat niet...

Bij voorbaat heel erg bedankt voor uw antwoord.
Katrij
Leerling bovenbouw havo-vwo - zaterdag 29 mei 2021

Antwoord

Heel plat gesproken: van rechts naar links over een kromme beweegt raak je eigenlijk oppervlakte kwijt. Als je dus integreert van $t=3$ tot $t=6$ krijg je een negatief antwoord: de gezochte oppervlakte met een minteken.

Je kunt de onderkant en de bovenkant ook apart parametriseren:

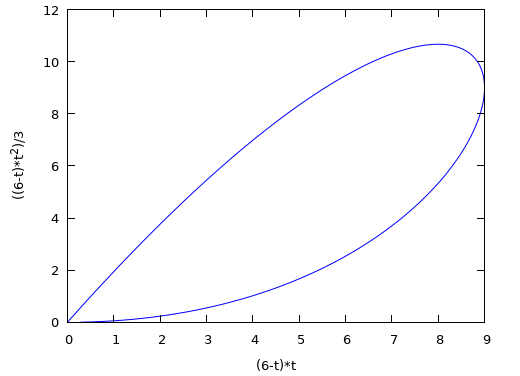
Voor de onderkant kun je de gegeven functies gebruiken met $0\le t\le3$.

Voor de bovenkant draai je de tijd om: neem vervang $t$ door $6-t$, want als $t$ van $0$ naar $3$ loopt beweegt $6-t$ van $6$ naar $3$ en dan beweegt het punt $\bigl(x(6-t),y(6-t)\bigr)$ dus bovenlangs van $(0,0)$ naar $(9,9)$.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 29 mei 2021