|
|
|
\require{AMSmath}



Inhoud onregelmatig viervlak
Een viervlak (tetraŽder) bestaat uit een gelijkzijdig driehoekig grondvlak met zijde 1 en drie opstaande zijden met lengte 1/√2.
Als antwoord geeft men voor de inhoud 1/12∑√12, terwijl ik als antwoord 3√/24 bekom.
Wie kan helpen?
Martin
3de graad ASO - vrijdag 7 mei 2021
Antwoord
Hallo Martin,
Jouw ruimtefiguur is niet een tetraŽder maar een piramide, zie de figuur hieronder.
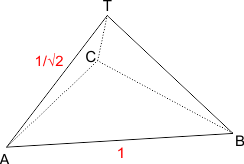
Om de inhoud te berekenen, hebben we de oppervlakte van het grondvlak nodig en de hoogte. Eerst maar eens het grondvlak, dit is de gelijkzijdige driehoek ABC met zijden 1:
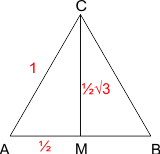
M is het midden van zijde AB. In driehoek AMC berekenen we de hoogte MC van deze driehoek: MC=1/2√3. Voor de oppervlakte van driehoek ABC vinden we dan:
Opp. ABC = 1/2∑1∑1/2√3 = 1/4√3.
Nu nog de hoogte van de piramide. Hieronder is de piramide nog eens getekend.
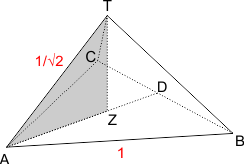
Z is het zwaartepunt van driehoek ABC. AD=1/2√3 (de hoogte van driehoek ABC), AZ is 2/3 deel hiervan. Dus:
AZ=2/3∑1/2∑√3
AZ=1/√3
Hieronder is de grijze driehoek AZT getekend:
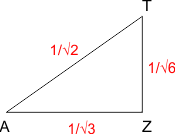
Met AZ=1/√3 en AT=1/√2 berekenen we de hoogte ZT van de piramide:
ZT=1/√6
Nu berekenen we de inhoud I van de piramide:
I=1/3∑G∑h
I=1/3∑1/4√3∑1/√6
I=1/12∑√(3/6)
I=1/24∑√2

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 7 mei 2021
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|













