WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Puntmuts in vorm van kegelmantel

Ik worstel met de volgende opgave:

Een puntmuts heeft de vorm van een kegelmantel en in de uitslag van deze kegelmantel is hoek ATA 90 graden. Verder geldt dat TA = 39 cm en dat AB = BC = CT. De puntmuts wordt versierd met 3 rode linten. Die linten worden gespannen om de mantel van A naar A, van B naar B en van C naar C.

Gevraagd: bereken de totale lengte van de de drie linten in cm nauwkeurig.

Ik heb dat als volgt gedaan: de omtrek van de cirkel is: 2 * ñ * 39 cm = 245,044227. 1/4 * 245,044727 = 61,26105675. Voor lint B geldt dan: 2/3 * 61,26105675 = 40,8407045 en voor lint C is dit: 1/3 * 61,26105675 = 20,42035225. Totale lengte is dan: 122,52 cm. Afgerond 123 cm. Het antwoorden boekje geeft echter aan 110 cm. Ik vraag me af wat ik hier niet goed doe. Als ik uitga van TA = 35 cm dan kom ik wel uit op 110 cm.
Joost
Iets anders - zaterdag 23 januari 2021

Antwoord

Hallo Joost,

Wanneer je een lint spant van A naar A', dan is de kortste afstand volgens een rechte lijn op de uitslag van de kegelsnede, zie onderstaande figuur.

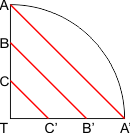
Op de puntmuts vormen de linten geen cirkels in het horizontale vlak. Tegenover de punten A, B en C kruipen de linten wat omhoog.

De totale lengte van de drie rode lijnen is afgerond 110 cm.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 23 januari 2021