WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Logaritmische ongelijkheden

Een vraag op een taak was: zoek de fout:

log(0.5)=log(0.5) $\Rightarrow$ 2.log(0.5)$<$3.log(0.5)
$\Rightarrow$ log(0.25)$<$log(0.125) $\Rightarrow$ 0.25$<$0.125

Mijn leerkracht schreef erbij dat log(0.5) negatief is, maar ik snap nog steeds niet waar de fout zit en wanneer het ongelijkheidsteken bij deze ongelijkheid moet wisselen.

Ine
3de graad ASO - zaterdag 24 oktober 2020

Antwoord

Hallo Ine,

Bij eenvoudige getallen kun je dit gemakkelijker zien:

2 is kleiner dan 3. Wiskundig geschreven: 2$<$3

Wanneer ik de getallen met een positief getal vermenigvuldig, bijvoorbeeld met 5, dan geldt nog steeds:

2·5$<$3·5, ofwel: 10 is kleiner dan 15.

Maar zodra ik vermenigvuldig met een negatief getal, dan is het anders:

2·-5$>$3·-5, ofwel: -10 is groter dan -15.

Op de getallenlijn is dit goed te zien, zie de figuur hieronder. Bij vermenigvuldigen met een negatief getal spiegelt het geheel ten opzichte van nul, dus 'groter dan' aan de positieve kant wordt 'kleiner dan' aan de negatieve kant:

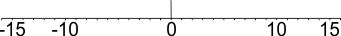
Conclusie:
Wanneer je bij een ongelijkheid links en rechts met een getal vermenigvuldigt, let dan goed op of dit getal positief of negatief is. Bij vermenigvuldiging met een negatief getal wisselt het ongelijkheidsteken. Men zegt vaak: 'Het teken klapt om'.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 24 oktober 2020