WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Eenheidscirkel

Leg met behulp van de eenheidscirkel uit waarom geldt:

tan(a) = sin (a) / cos (a)
Anne v
Leerling bovenbouw havo-vwo - zondag 23 juni 2019

Antwoord

Hallo Anne,

Hieronder zie je de eenheidscirkel (dus: straal = 1), met daarin de rechthoekige driehoek ABC:

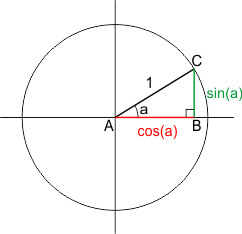
De sinus van hoek a is ^BC/_AC. Omdat AC=1, is zijde BC gelijk aan de sin(a). Het groene lijnstuk heeft dus de lengte sin(a).
Op dezelfde manier vind je dat de lengte AB (het rode lijntje) gelijk is aan cos(a).
Hoe vind je ook alweer de tangens van een hoek in een rechthoekige driehoek?
Welke zijden moet je dus in driehoek ABC op elkaar delen om tan(a) te vinden?
Zie je nu dat geldt: tan(a) = ^sin(a)/_cos(a)?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 23 juni 2019