WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Drie middelloodlijnen snijden in één punt

Hallo,
Ik heb een vraag over het bewijzen van lijnen in driehoeken..
Ik ben bezig met het bewijzen dat drie middelloodlijnen elkaar snijden in één punt..
Ik heb hierbij gewoon driehoek ABC getekend met de middelloodlijnen en AM=BM, AM=AC en BM = BC
En dan zag ik gewoon:

M,ac is loodrecht op AC en geldt CM=AM
M,ab is loodrecht op AB en geldt AM=CM
M,cb is loodrecht op CB en geldt CM=BM
Dus snijden de drie middelloodlijnen elkaar.

Maar in mijn boek staat het nu al voor een aantal bewijzen, met in dit geval een driehoek waarbij ze géén middelloodlijn tekenen en het vervolgens bewijzen. Maar doe ik het dan niet goed? Ik bewijs het met mijn bewijs toch ook?..

Hetzelfde geldt voor de bissectrices gaan door één punt:
Het boek geeft dan:
Met een tekening met weer een hoek zonder bissectrice getekend.
In driehoek ABC snijden k en l elkaar in N (de bissectrices)
N op k, dus d(N,AB) = d(N,AC)
N op l, Dus d(N,AB)= d(N,BC) Dus d(n,AC) = d(n,BC)
Dus N ligt op de bissectrice van hoek C dus gaan de bissectrices door één punt

Hoe ik zou bewijzen:
Alle drie de bissectrices tekenen
d(N,AB) = d(N,AC)
d(N,AB) = d(N,BC)
d(N,AC) = d(N,BC)
Dus de drie bissectrices gaan door één punt.

Doe ik dan toch iets fout met mijn bewijzen?

Vriendelijke groet,
Stijn
Stijn
Cursist vavo - donderdag 9 mei 2019

Antwoord

Hallo Stijn,

Allereerst denk ik dat je driehoek ABC hebt getekend met de middelloodlijnen en AM=BM, AM=MC (in plaats van AM=AC) en BM=MC (in plaats van BM=BC):

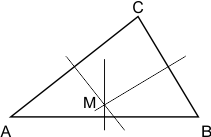
Met jouw wijze van redeneren zou ik kunnen bewijzen dat de vier middelloodlijnen van een vierhoek ook door één punt gaan:

Gegeven de vierhoek ABCD:

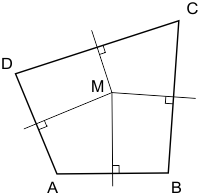
M,ab is loodrecht op AB en dan geldt AM=BM
M,bc is loodrecht op BC en dan geldt BM=CM
M,cd is loodrecht op CD en dan geldt CM=DM
M,da is loodrecht op DA en dan geldt DM=AM

De middelloodlijnen gaan door één punt.

Maar in deze figuur zien we dat dit niet zomaar klopt. De middelloodlijnen van deze vierhoek gaan zeker niet door één punt:

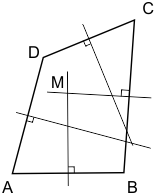
Bij mijn 'bewijs' gaat het mis omdat ik uitga van een vierhoek waarvan de middelloodlijnen door één punt gaan. Dan zal de conclusie ook zijn dat de middelloodlijnen door één punt gaan. Een cirkelredenering, dus.

Laten we eens kijken waar het lek in het bewijs zit:
M,ab is loodrecht op AB en dan geldt AM=BM
Eigenlijk gaat het hier al mis: punt M is niet (goed) gedefinieerd. Maar goed: voor elk punt M op de middelloodlijn van AB geldt AM=BM.
M,bc is loodrecht op BC en dan geldt BM=CM
Hier geldt hetzelfde bezwaar, maar we bedoelen natuurlijk:
M is het snijpunt van deze twee middelloodlijnen. Dus:
AM=BM, BM=CM, dus ook: AM=CM.
Tot zover gaat het goed, dit geldt ook in de onderste figuur. Maar dan:
M,cd is loodrecht op CD en dan geldt CM=DM
Hier gaat het echt mis. Waarom zou de middelloodlijn van CD ook door punt M gaan? In de onderste figuur zien we duidelijk dat dit niet zomaar het geval is. Het bewijs is niet waterdicht en dus niet geldig.
Ook bij jouw bewijs beweer je 'zomaar' dat de derde middelloodlijn door punt M gaat. Je gaat hier dus van uit, maar dit is nu juist wat je moet bewijzen.

Hoe dan wel? Een correct bewijs is als volgt:
We beschouwen een driehoek ABC. De lijn l is de middelloodlijn van AB. (Dus voor elk punt P op l geldt: AP=BP).
De lijn m is de middelloodlijn van BC. (Dus voor elk punt Q op l geldt: BQ=CQ).
S is het snijpunt van l en m. Omdat S op l ligt, geldt: AS=BS. Omdat S op m ligt, geldt: BS=CS. Dan geldt ook: AS=CS.
Een definitie van de middelloodlijn van AC is: 'De verzameling punten op gelijke afstand van A en C'. We hebben zojuist aangetoond dat de afstand van S tot de punten A en C gelijk is. Daarom is S een punt van de middelloodlijn van AC. Alle drie de middelloodlijnen gaan door S.
Kan je nu zelf een waterdicht bewijs opstellen voor de bewering dat de drie bissectrices door één punt gaan?

Bonusvraag: welke bijzondere eigenschap hebben de hoekpunten ABCD van een vierhoek wanneer de vier middelloodlijnen van de zijden door één punt gaan?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 10 mei 2019