WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Maximale lengte

Hallo,

Ik loop bij een opgave over het berekenen van de maximale lengte vast. Ten eerste is het mij eigenlijk niet echt duidelijk, wat ze willen dat ik ga berekenen? Willen ze het stuk A tot punt Z (fictief), Z staat dan loodrecht onder P?

Verder zag ik bij de uitwerkingen dat ze da/dx gebruiken, maar dat is mij eigenlijk niet helemaal duidelijk waarom ze een afgeleide gebruiken? Ik dacht dat je dit met een meetkundige vergelijking kon oplossen, maar ze berekenen de afgeleide naar 0. En hiermee berekenen ze x.

En uiteindelijk nemen ze voor het eindantwoord de x + (√5 · -x - (x)²). En die laatste regel snapte ik helemaal niet. Ik hoop dat iemand mij hierbij kan helpen?

Mvg,
Anna
Anna
Leerling bovenbouw havo-vwo - vrijdag 13 april 2018

Antwoord

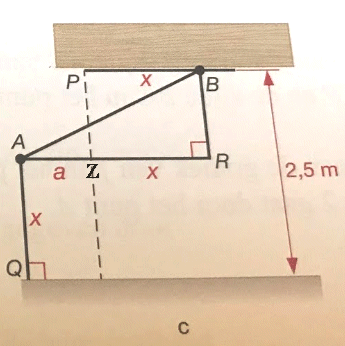
In driehoek ARB is AZ gelijk aan $a$. Die $a$ is de lengte van het stuk van de garagedeur dat uitsteekt. In deze rechthoekige driehoek geldt:

$AR^2+BR^2=AB^2$

Invullen geeft:

$(a+x)^2+(2,5-x)^2=2,5^2$

Je kunt nu $a$ uitdrukken in $x$. Oplossen naar $a$ (zie uitwerkingenboek) geeft:

$
a = - x + \sqrt {5x - x^2 }
$

Je hebt nu $a$ geschreven als functie van $x$. Je wilt weten voor welke waarde van $x$ die $a$ maximaal is. Dat is dan een kwestie van de afgeleide bepalen, de afgeleide nul stellen, grafiek plotten en vaststellen of er sprake is van een maximum of minimum. Een optimaliseringsprobleem dus...

De afgeleide wordt:

$
\eqalign{a' = - 1 + \frac{{5 - 2x}}
{{\sqrt {5x - x^2 } }}}
$

Op nul stellen en oplossen geeft als mogelijke kandidaat voor een extreem:

$
\eqalign{x = \frac{5}
{2} - \frac{{5\sqrt 2 }}
{4}}
$

Als je (met een schets/plot/tekenverloop) hebt vastgesteld dat het maximum bij deze $x$-waarde wordt aangenomen vul je de $x$-waarde in bij de functie. Dat geeft je dan de maximale waarde voor $a$:

$\eqalign{a=-\left({\frac{5}{2}-\frac{{5\sqrt2}}{4}}\right)+\sqrt{5\left({\frac{5}{2}-\frac{{5\sqrt2}}{4}}\right)-\left({\frac{5}{2}-\frac{{5\sqrt2}}{4}}\right)^2}\approx{\text{1}}{\text{,04}}}$

Opgelost!

Je moet maar even aangeven waar en/of wat er nog iets onduidelijk is. Hopelijk helpt dat.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 14 april 2018

Re: Maximale lengte