WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Halfvlakken

Ik snap niet hoe op het antwoord/de uitwerking gekomen is bij voorbeeld 2 over begrensde gebieden, hoe worden deze ongelijkheden opgesteld of is dit meer een uitleg als aanvulling op het boek van Getal & Ruimte?
grafieken en gebieden

Sterre
Leerling bovenbouw havo-vwo - woensdag 4 april 2018

Antwoord

Voorbeeld 2

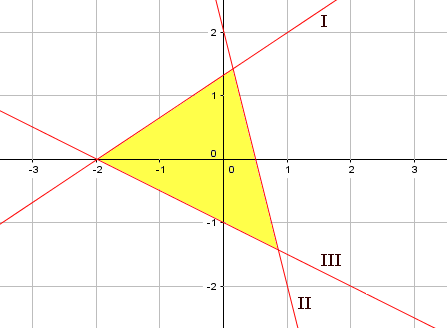
In voorbeeld 2 zie je 3 lijnen lopen. In hoofdstuk 5 had je al kennis gemaakt met formules voor rechte lijnen.
lineaire vormen
Hier zou je dan moeten proberen de formules voor de lijnen te vinden en te bepalen of het gebied hoort bij 'groter dan' of bij 'kleiner dan'. Dat is nog wel een lastig klusje.

Lijn I
Lijn I gaat door (-2,0) en (1,2). Vorig jaar heb je geleerd hoe je een formule van een rechte lijn kunt opstellen aan de hand van twee gegeven punten. Richtingscoëfficiënt en het snijpunt met de y-as:
lineaire formules opstellen
In dit geval gaat dat zo:

$
\eqalign{
& a = \frac{{y_A - y_B }}
{{x_A - X_B }} = \frac{{0 - 2}}
{{ - 2 - 1}} = \frac{{ - 2}}
{{ - 3}} = \frac{2}
{3} \cr
& y = \frac{2}
{3}x + b \cr
& {\text{Vul}}\,\,{\text{(1}}{\text{,2)}}\,\,{\text{in}}\,{\text{:}} \cr
& 2 = \frac{2}
{3} \cdot 1 + b \Rightarrow b = 1\frac{1}
{3} \cr
& {\text{Formule}}\,\,{\text{van}}\,\,{\text{lijn}}\,\,{\text{I:}}y = \frac{2}
{3}x + 1\frac{1}
{3} \cr}
$

Je kunt nu de formule 'omwerken' tot '...x+...y=...'. Dat gaat zo:

$
\eqalign{
& y = \frac{2}
{3}x + 1\frac{1}
{3} \cr
& 3y = 2x + 4 \cr
& - 2x + 3y = 4 \cr
& 2x - 3y = - 4 \cr}
$

De vraag is dan of het $\ge$ of $\le$ moet zijn. Als je O(0,0) invult dan komt er $0$ uit en dat is groter dan $-4$ dus:

$
2 \cdot 0 - 3 \cdot 0 = 0 \Rightarrow 2x - 3y \geq - 4
$

Je hebt nu de ongelijkheid die hoort bij lijn I.

Op dezelfde manier kan je dat voor lijn II en III doen.
Zou dat lukken?

Probeer het! Anders nog maar even verder vragen!

PS
De website is een samenvatting voor HAVO wiskunde A. Je kunt er naast een overzicht van de leerstof voorbeelden, uitwerkingen en uitleg vinden.
HAVO wiskunde A

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 4 april 2018