WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Oppervlakte

Dit is een reactie op vraag 85850

Dankuwel!! Alleen hoe kan ik een schets maken, want in mijn f(x) staan die a's dus hoe zet ik die in mijn GR?
Kaylee
Leerling bovenbouw havo-vwo - dinsdag 13 maart 2018

Antwoord

Hallo Kaylee,

Inderdaad, je kunt geen formule met een parameter in je rekenmachine invoeren. Nu komt het aan op eigen inzicht. Als eerste: het gaat ons om de driehoek OAB. We kennen inmiddels de (formules voor) de coördinaten van deze punten. De oorspronkelijke functie hebben we dus niet meer nodig!

De punten waar het om gaat, zijn:
O(0 ; 0)
A(a ; 1+2,5a³)
B(2a ; 1+2a³)

Deze kunnen we in een schets weergeven, gewoon met potlood en lineaal. Weet je mijn hint nog dat bekend is: a$>$0? Dan zijn de x-coördinaten van A en B positief. Verder ligt A hoger dan B, want de y-coördinaat van A (1+2,5a³) is groter dan de y-coördinaat van B (1+2a³). De schets ziet er dan zo uit:

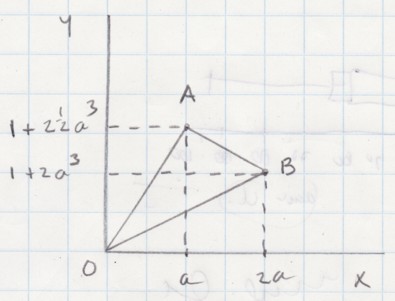
Het hoeft allemaal niet op schaal, het gaat erom dat je ziet hoe punten ten opzichte van elkaar liggen, en hoe driehoek OAB er kennelijk ongeveer uitziet. Ik heb bijvoorbeeld punt A duidelijk hoger getekend dan punt B, zodat je goed ziet welke lijnstukken horizontaal, verticaal of schuin lopen.

Helaas is driehoek OAB geen 'mooie' driehoek, met bv een horizontale of verticale zijde. In zo'n geval bepalen we de oppervlakte van OAB door hulplijnen te tekenen (zodat we rechthoekige driehoeken en/of rechthoeken krijgen), en op een handige manier oppervlaktes van deze driehoeken en rechthoeken bij elkaar op te tellen of van elkaar af te trekken. Kan jij bijvoorbeeld verzinnen hoe je de oppervlakte van de rechthoekige driehoek onder OA zou berekenen?

Tip: bedenk hoe je dit zou doen wanneer bv a=2. In dat geval zijn de coördinaten van A (2 ; 21), reken maar na. Voer nu dezelfde berekening uit met a. Je krijgt niet een concrete waarde voor de oppervlakte, maar een formule.

Probeer dan de oppervlakte van driehoek OAB uit te drukken in de som (of verschil) van meerdere oppervlakken, dus de som (of verschil) van meerdere formules met a. Zo kom je tot een totale formule voor de gevraagde oppervlakte.

Nu jij weer!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 13 maart 2018