WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Cirkels in een rechthoek

Dit is een reactie op vraag 76943

Het probleem is eigenlijk iets ruimer. De pallet (waar de rollen opstaan) is een vast gegeven. De roldiameter varieert. B.v. palletafmeting = 1500mm x 800mm. Roldiameter = 170mm. Hoeveel rollen gaan er op de pallet (recht of genest)

Dirk d
Iets anders - donderdag 21 april 2016

Antwoord

Hallo Dirk,

Ik kan me niet voorstellen dat er een algemene formule is om te berekenen hoeveel cirkels (rollen) met gegeven diameter D passen in een rechthoek (pallet) met gegeven lengte L en breedte B. Ik kan wel een procedure bedenken hoe dit aantal berekend kan worden.
Hieronder heb ik een rechthoek getekend met lengte L en breedte B. Vanuit de hoek links onder is deze gevuld met cirkels met straal r, de cirkels zijn zo dicht mogelijk op elkaar gepakt. In het algemeen blijven langs de rechter zijde en bovenzijde marges over. De marge rechts noem ik m:

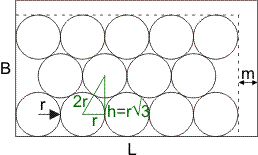
De verticale afstand tussen middellijnen van de cirkels noem ik h, zie het groene driehoekje. Deze afstand h is te berekenen met Pythagoras:

r² + h² = (2r)²
h² = 4r² - r² = 3r²
h = r√3

Wanneer we de cirkels wat uit elkaar schuiven, kunnen we h kleiner maken. wellicht geeft dit ruimte voor een extra rij aan de bovenkant. Onderstaande figuren tonen de situatie waarbij de marge verdeeld is over tussenruimtes tussen de cirkels:

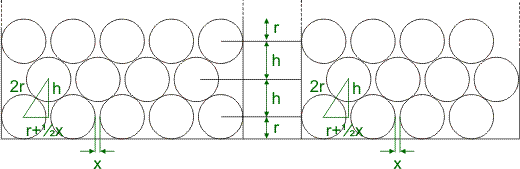
Links geeft de situatie weer waarbij de rest van L/r kleiner is dan ¹/₂. In de tweede rij past dan een cirkel minder dan in de eerste rij. Rechts is deze rest groter dan ¹/₂, het aantal cirkels in alle rijen is gelijk.

Nu gaan we rekenen:
Het aantal cirkels in de onderste twee rijen noem ik n. In de tekeningen is n gelijk aan 9 resp. 8. Dit aantal bereken je met:

n = ^L/_R - ¹/₂

waarbij n altijd naar beneden moet worden afgerond.

De ruimte tussen twee cirkels noem ik x. Elk van deze cirkels (via een zig-zag-route van links naar rechts) wordt ¹/₂x verschoven ten opzichte van de voorgaande cirkel. Er moeten (n-1) cirkels worden opgeschoven (de eerste cirkel blijft op zijn plaats). De verschuiving van de laatste cirkel is zodoende ¹/₂x·(n-1). Wanneer we de marge m netjes verdelen, dan berekenen we x met:

¹/₂x·(n-1) = m
x = 2m/(n-1)

In het driehoekje rechts berekenen we de nieuwe waarde voor h met behulp van Pythagoras:

h²+(r+¹/₂x)² = (2r)²
h²+r²+rx+¹/₄x² = 4r²
h² = 3r²-rx-¹/₄x²
h = √(3r²-rx-¹/₄x²)

Nu kunnen we berekenen hoeveel rijen in de breedte van de rechthoek passen:
De hoogte van een aantal rijen berekenen we door te bedenken dat:
De hoogte tot het eerste middelpunt gelijk is aan de straal r,
Voor elke volgende rij een hoogte h wordt toegevoegd tot het volgende middelpunt,
Vanaf het laatste middelpunt nog een hoogte r volgt tot de rand
De hoogte van m rijen wordt zodoende:

hoogte m rijen = 2r + (m-1)·h

Deze hoogte mag niet meer zijn dan de breedte B van de pallet:

2r + (m-1)·h = B
(m-1)·h = B-2r
m-1 = (B-2r)/h
m = (B-2r)/h + 1

Het aantal rijen dat op de pallet past, is gelijk aan de waarde m die je met deze formule berekent, waarbij altijd naar beneden afgerond moet worden. Voor het berekenen van het totaal aantal rollen moet je nog even bedenken of alle rijen hetzelfde aantal rollen heeft (zoals in de rechter figuur) of elke 2e rij een rol minder heeft (zoals in de linker figuur).

Met deze procedure kan worden onderzocht of het zin heeft om rollen een stukje uit elkaar te plaatsen om zodoende ruimte voor een extra rij te maken. Ik weet niet of je de rollen het beste in de lengterichting of in de breedterichting van de pallet uit elkaar kunt plaatsen. Door verwisselen van L en B kan je beide mogelijkheden onderzoeken.

Wanneer beide mogelijkheden niets extra's opleveren, kan je nog proberen om de eerste rol van de laatste rij geheel in de linker bovenhoek te plaatsten, en volgende rollen zo goed mogelijk aan te schuiven, zie de figuur hieronder. Wellicht past uiteindelijk een rol extra op de pallet. Mijn gevoel zegt dat dit niets oplevert, maar ik kan het niet aantonen.

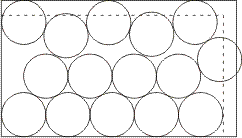
Aanvulling:

Een mede-beantwoorder wees op nog een andere mogelijkheid, zie onderstaande figuur. Hier zijn de cirkels in lengterichting (nagenoeg) opgesloten, en elke tweede rij heeft een cirkel minder dan de eerste rij.

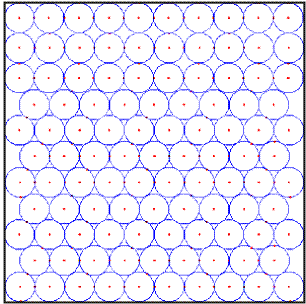
De cirkels zijn in de meest compacte vorm gestapeld. In verticale richting kan dan nog wat marge over zijn. In deze situatie kan het voorkomen dat de laatste korte rij recht boven de rij eronder geplaatst wordt. Dit kost wat extra ruimte (deze is hier ook beschikbaar), maar deze korte rij kan met een extra cirkel worden aangevuld tot een lange rij. Dat scheelt weer één cirkel!

Kortom: geen éénduidige formule voor alle mogelijke situaties, wel enkele concrete procedures die bv. in Excel geprogrammeerd zouden kunnen worden.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 24 april 2016