WisFaq!

Loading jsMath...

De digitale vraagbaak voor het wiskundeonderwijs

HOME

\require{AMSmath}

Sinusregel in koordenvierhoek

Stel koordenvierhoek ABCD. Diagonalen AC en BD.
Ik kom niet uit het volgende probleem: stel hoek(A)=90 graden. Het blijkt dat BD / sin(hoek(A)) = AC / sin(hoek(A)-hoek(CAD))
Hoe is dat te verklaren?

Herman
Ouder - zondag 19 januari 2014

Antwoord

Beste Herman,

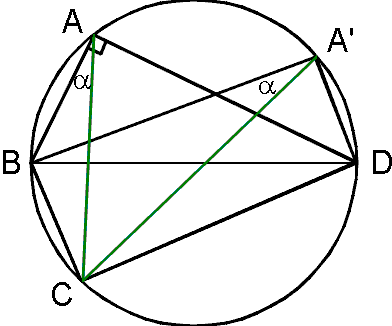
Uit \angleA=90° volgt: sin(\angleA)=1

Verder zien we in de figuur:
\angleA-\angleCAD = \angleBAC, deze hoek noem ik \alpha

Jouw bewering wordt dan:

BD = AC/sin\alpha ofwel:

AC = BD×sin\alpha

Dit kan niet waar zijn: in de figuur heb ik twee posities voor punt A gekozen (A en A'). Hoek \alpha blijft constant (gelijke koorden hebben gelijke omtrekshoeken). BD en sin\alpha zijn constant, maar duidelijk is dat AC en A'C niet even lang zijn, dit is in strijd met jouw uitspraak.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 19 januari 2014