WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

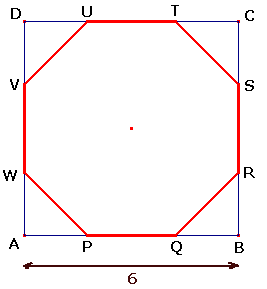
Een vierkant waar de achthoek precies in past

Van het vierkant ABCD met zijde 6 worden bij de hoekpunten driehoeken weggelaten zodat een regelmatige achthoek ontstaat. De opdracht is nu om de zijde van de achthoek te berekenen. Ik dacht zelf dat je gewoon 6 kon delen door 3 om de zijde te weten, maar dat lijkt me dan weer zo makkelijk gedacht dus verwacht ik niet dat het goed is.

Maar nu weet ik niet hoe ik anders te werk moet gaan, want je hebt bijna geen gegevens...
Atena
Leerling bovenbouw havo-vwo - maandag 6 januari 2014

Antwoord

Maak eerst een tekening:

Neem AP=x. Er geldt dan: PQ=6-2x. Ga na!
In driehoek APW geldt: x²+x²=(6-2x)². Waarom?
Die vergelijking kan je oplossen! Doen!
Je vindt dan x=6-3√2.
PQ=6√2-6.

Opgelost!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 6 januari 2014