WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Overgangsmatrices (2)

Oefening
Wanneer een bepaald dier in een nieuw leefgebied terechtkomt, dan moet het zich aanpassen aan de omstandigheden. Er zijn plaatsen waar zo’n dier kan drinken en plaatsen waar het zijn voedsel vindt. Gedurende de dag zwerft het voortdurend tussen die plaatsen heen en weer, waarbij langzamerhand een vast patroon gaat ontstaan. De nachten blijven buiten beschouwing, omdat het dier dan niet actief is. Stel dat er één drinkplaats D is en twee plaatsen om voedsel te halen, A en B. Een bioloog noteert steeds om het uur waar hij het dier aantreft, bij D, bij A of bij B. Op grond daarvan maakt hij de de graaf die je hieronder ziet.
Maak bij deze graaf een overgangsmatrix M.
Op zeker moment is het dier aan het drinken. Geef dit weer in een kolommatrix P₀.
Bereken P1=M⋅P₀. Welke betekenis heeft de matrix P₁?
Bereken op dezelfde wijze de matrix P₂.
Vanaf welke waarde van n geldt: M·P_n=P_n?
Hoeveel procent van zijn actieve tijd brengt het dier op den duur op elk van de plaatsen D, A en B door?
Zijn overgangsmatrix is
 40   20   20
 30   40   30
 30   40   50
Maar bij b heb ik dan de kolom ( 0, 0, 1)
Bij c bekom ik de kolom ( 20, 30, 50 )
Hoe begin ik aan vraag f?

Alvast bedankt

Er is dus geen graaf maar wel de overgangsmatrix, misschien moet ik deze in procenten plaatsen?

Mijn vraag is dus dat ik bij c na het maken van het product ( 20, 30, 50 ) bekom. Wil dit zeggen dat na 1 dag er 20 dieren op plaats A staan, 30 dieren op plaats B en 50 op D?
Maar na 2 dagen krijg je dan ( 2400, 3300, 4300 )?
Dina
3de graad ASO - dinsdag 3 december 2013

Antwoord

Volgens mij gaat het om deze graaf:

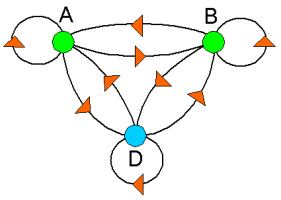
De bioloog heeft de dieren geteld:

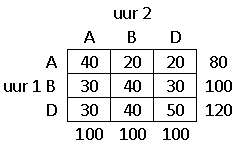
De vraag is nu om een overgangsmatrix te maken. Dat ziet er dan zo uit:

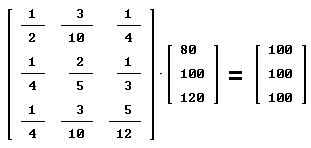
Links staat de overgangsmatrix met daarnaast de kolommatrix. Rechts staat dan het resultaat na een uur.

...en dan mag je de rest zelf nog 's proberen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 3 december 2013