|
|
|
\require{AMSmath}



Rechthoek in vieren verdeeld
Ik heb nog een vraagje over een rechthoek deze is in vieren verdeeld, dus 4 driehoeken erin met in het midden punt s. En deze is niet op ware grootte getekend!
gegeven ŠLMO = 42° en vierhoek LMNO is een rechthoek. Verder moet ik alle hoeken berekenen dus LOM,NOM,NMO,LSM,OSN,NSM, maar hoe? (Volgens mij heb je normaal gesproken in een rechthoek vier gelijke hoeken van 90°.
ŠLMO is de helft zeg maar van de rechthoek.
Is ŠNOM dan ook 42°? Hopelijk kunt u helpen, heb eventueel ook een tekening.
Yvette
Iets anders - dinsdag 9 juli 2013
Antwoord
Hallo Yvette,
Ik begrijp dat dit de figuur is:
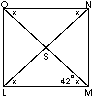
LM en ON zijn evenwijdig, dus de hoeken LMO en NOM zijn Z-hoeken, dus gelijk. Verder zie je dat allevier de driehoeken gelijkbenig zijn: LS=MS=NS=OS. Elke driehoek heeft dus twee gelijke basishoeken. Conclusie: alle hoeken met een X zijn gelijk, dus 42°.
Verder weet je al:
- de hoeken van de rechthoek zijn 90°;
- de som van de hoeken van elke driehoek 180°;
- bij punt S zijn de overstaande hoeken gelijk;
- bij punt S zijn elke twee hoeken die naast elkaar liggen samen 180° (gestrekte hoek)
Hiermee heb je ruim voldoende informatie om alle hoeken te berekenen, denk ik. Lukt het zo?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 9 juli 2013
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










