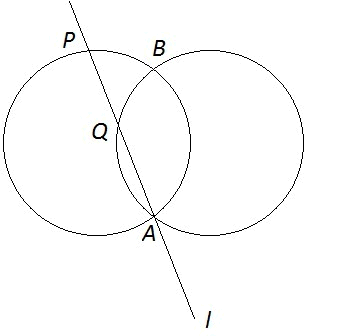WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Gelijkbenigheid bewijzen

Dit is een reactie op vraag 67251

oke dat het een ruit was had ik inderdaad niet gezien, moet daar ook een bewijs voor worden geleverd?

Dus de volgende uitwerking is dus foutloos voor de hele opgave? (het is namelijk voor een cijfer)
AC₁BC₁ is een ruit
Dus AC₁B en AC₂B zijn gelijk.
De kleine bogen AB zijn gelijk.
$\angle$P=$\angle$Q (omtrekshoek)
$\angle$P=¹/₂boogAB (op cirkel C₁
$\angle$Q=¹/₂boogAB (op cirkel C₂
boog AB op C₁ = boog AB op C₂
DBPQ = gelijkbenig (BP=BQ)

PS we kregen onderstaande tekening.
Daar zijn geen middelpunten geven, mag ik daar dan gewoon concluderen dat het een ruit is?

Johnny
Leerling bovenbouw havo-vwo - donderdag 29 maart 2012

Antwoord

Dag Johnny,
Natuurlijk mag je direct besluiten tot: AC₁BC₂ is een ruit
Want uit het gegeven volgt AC₁ = C₁B = BC₂ = C₂A (gelijke lijnstukken; stralen).
En het bewijs is het wel ongeveer, echter alleen passend bij de tekening die bij MIJN eerste antwoord staat.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 29 maart 2012