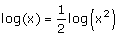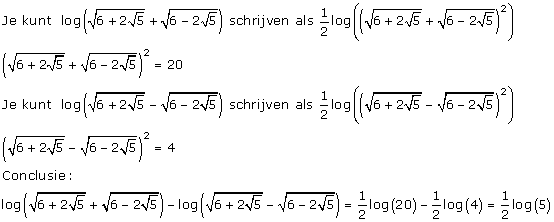|
|
|
\require{AMSmath}



Logaritmische vergelijking
Hallo, ik moet voor een taak een logaritmische vergelijking bewijzen. Ik heb dit helemaal opgelost maar kom verkeerd uit, zouden jullie eens willen kijken waar ik eventueel een fout zou kunnen gemaakt hebben? En misschien liefst eens heel de oefening uitschrijven? Alvast bedankt en hier komt de oefening:
1/2log5=log($\sqrt{ }$(6+2$\sqrt{ }$5))+$\sqrt{ }$(6-2$\sqrt{ }$5)))-log($\sqrt{ }$(6+2$\sqrt{ }$5))-$\sqrt{ }$(6-2$\sqrt{ }$5)))
Een kleine duiding bij de oefening: die 6+ 2$\sqrt{ }$5 of 6-2$\sqrt{ }$5 staan allebei onder dezelfde vierkantswortel, dus eens volluit gezegd voor de eerste is het: de wortel van zes plus 2vierkantswortel 5 + de wortel van zes min 2 vierkantswortel 5! dus niet: vierkantsworel 6 plus 2wortel 5.
groetjes
eva
3de graad ASO - zondag 30 januari 2011
Antwoord
Volgens mij kloppen de haakjes nog steeds niet helemaal, maar ik geloof dat ik er uit ben:
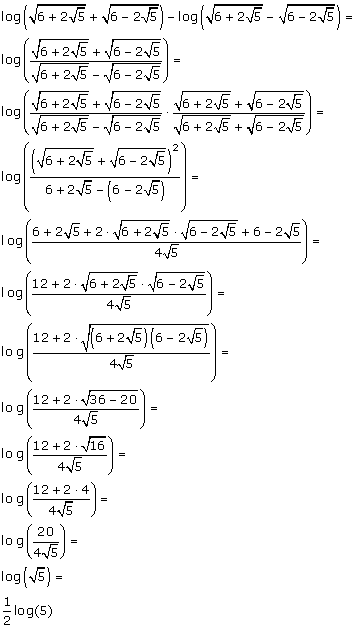
Dat moet kunnen! Leuk wel... hopelijk helpt het. Leuk wel... hopelijk helpt het.
Leermomenten:- Op het goede moment de rekenregels van de logaritme toepassen
- De worteltruuk! Hoe werk je wortels in de noemer weg?
- Ken uw meerkwaardige producten
- ...
Meer leermomenten? Misschien kan het wel makkelijker!:-)
Je kunt ook gebruik maken van:
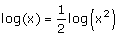
Je krijgt dan zoiets als:
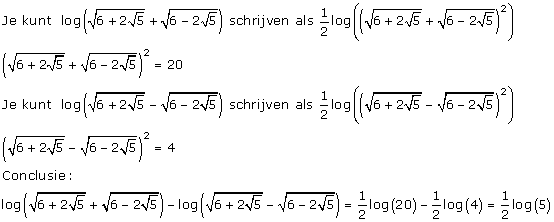
...en dat is veel eleganter:-)
Met dank aan kp.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 30 januari 2011
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








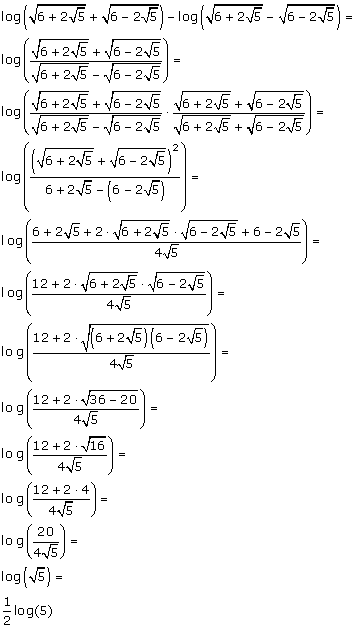
 Leuk wel... hopelijk helpt het.
Leuk wel... hopelijk helpt het.