WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Binair delen

Hoi, nou ben ik 38 jaar, doe nu (helaas wat laat) mijn hbo, stam uit de tijd dat je wel staartdelingen leerde op school en de decimale staartdeling ben ik nog steeds machtig, echter van binair delen snap ik helemaal niets en aangezien ik dit eerdaags op mijn tentamen ga krijgen, hoop ik dat jullie het me duidelijk kunnen maken c.q. krijgen.

Neem deze bv:
1010/1101110\1011





     1010





   - ----
ik zou zeggen dat gaat 1 keer en wordt dan:
     0111
Vervolgens moet ik de 1 op de 5de positie lenen, want ik kan niet delen (=0)
dus:
     01111





      1010





    - ----





dat gaat 1 keer





      0101
nu leen ik de 1 op de 6de positie
dus:
       1011





       1010





     - ----





       0001
oftwel even netjes:
1010/1101110\10101





     1010    ^------ 1x





   - ----





     0111





     0000     ^----- 0x, dus de 1 van 5de positie lenen





    - ----





      1111  





      1010     ^---- 1x





    - ----





      0101





      0000      ^----- 0x, dus de 1 van 6de positie lenen





    - ----





       1011





       1010      ^--- 1x





     - ----





       0001





       0000       ^----- 0x, dus 0 op 7de positie lenen





     - ----





          10
Dit gaat ook 0x (nul keer) dus dan krijg je de komma dacht ik zo en ga je verder met nullen lenen zover als je wilt

volgens mijn boek gsat het echter zo:
1010/1101110\1011
     1010
     ----
     0111
Waarom wordt er hier 1 plaats naar rechts gesprongen? of is de uitkomst 011 en leen je de 1 op de 5de positie al hier?
     0000 
     ----
      
      1111  welke 1 wordt hier geleend? 
      
      1010
      ----
       1010
       1010
       ----
       
       0000
Mijn conclusie: of ik doe iets fout of het boek en de leraar hebben het fout. Ik vermoed het eerste
remco
Student hbo - donderdag 21 oktober 2010

Antwoord

Dag Remco,
Misschien helpt het om de staartdeling netjes onderelkaar te schrijven:

Ik noem de posities van rechts naar links, te beginnen met de 0e positie.
Na de eerste stap blijft er na aftrekken 11 over. Je haalt dan een 1 aan (2e positie) en dan gaat het 0 keer.
Dan haal je nog een 1 aan (1e positie) en heb je 1111.
Nu gaat het weer 1 keer, verschil=101. Dan haal je de laatste 0 aan (0e positie)en gaat het 1 keer.
Jouw vermoeden dat de leraar gelijk heeft klopt dus wel.
Ik denk dat je bij het aftrekken iets fout doet.
Laat maar horen als het nog niet duidelijk is.
Groeten,
Lieke.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 22 oktober 2010

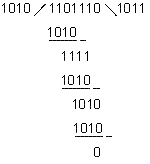
Re: Binair delen