WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Grootste oppervlakte vierhoek

Hoe kun je bewijzen dat van alle vierhoeken met dezelfde omtrek het vierkant de gootste oppervlakte heeft?
Marco
Leerling bovenbouw havo-vwo - woensdag 21 januari 2009

Antwoord

Beste Marco,
Allereerst zal die vierhoek convex zijn, immers als er een hoek naar binnen steekt is het oppervlak altijd kleiner dan als diezelfde hoek naar buiten steekt.
Stel dat we beginnen met het kiezen van de lengte van een van de diagonalen.
Binnen zekere grenzen is dat altijd mogelijk. Teken hem horizontaal.
Op die diagonaal zetten we boven en onder twee driehoeken. Boven: zijden a en b en onder c en d.
Als we kiezen voor een totale lengte van a+b, dan ligt het hoekpunt op een ellips met brandpunten aan de uiteinden van de diagonaal. Het maximale oppervlak van die direhoek krijgen we als het hoekpunt recht boven het midden van de diagonaal ligt, immers dat is het "hoogste " punt van die ellips.
Conclusie: Voor een maximaal oppevlak moeten we die twee driehoeken gelijkbenig maken.
We hebben nu dus in elk geval een vlieger. Zie figuur.

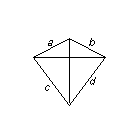
Nu kennen we de lengte van a+d en ook b+c (=halve omtrek vierhoek).
Kijken we nu naar de driehoeken met de verticale diagonaal en bijvoorbeel a en d, dan moeten we ook a en d gelijk kiezen, net als b en c.
Nu hebben we een ruit.
De laatste stap: Bewijs dat een ruit een maximaal oppervlak heeft als de hoeken recht zijn, ofwel een vierkant.
Kan je die laatste stap zelf als je bedenkt hoe je het oppervalk van een ruit berekent en dan met wat algebra afronden?
Succes, Lieke.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 24 januari 2009